
【题目】如图①,某超市从一楼到二楼有一自动扶梯,图②是侧面示意图.已知自动扶梯AB的坡度为1∶2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ , C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN , 在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )
A.10.8米
B.8.9米
C.8.0米
D.5.8米
【答案】D
【解析】解:延长CB交PQ于点D. 
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴ ![]() =
= ![]() =
= ![]() .
.
设BD=5k(米),AD=12k(米),则AB=13k(米).
∵AB=13(米),
∴k=1,
∴BD=5(米),AD=12(米).
在Rt△CDA中,∠CDA=90゜,∠CAD=42°,
∴CD=ADtan∠CAD≈12×0.90≈10.8(米),
∴BC=10.8﹣5≈5.8(米).
故答案为:D.
延长CB交PQ于点D.根据平行线的性质得出BC⊥PQ.根据坡度的定义得出![]() =
=![]() ,根据勾股定理设BD=5k(米),AD=12k(米),则AB=13k(米).又AB=13(米),从而算出BD,AD的长,在Rt△CDA中根据正切函数的定义得出CD=ADtan∠CAD,进而得出BC的长。
,根据勾股定理设BD=5k(米),AD=12k(米),则AB=13k(米).又AB=13(米),从而算出BD,AD的长,在Rt△CDA中根据正切函数的定义得出CD=ADtan∠CAD,进而得出BC的长。


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED.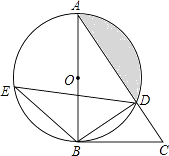
(1)如果∠CBD=∠E,求证:BC是⊙O的切线;
(2)当点E运动到什么位置时,△EDB≌△ABD,并给予证明;
(3)在(1)的条件下,若tanE= ![]() ,BC=
,BC= ![]() ,求阴影部分的面积.(计算结果精确到0.1)
,求阴影部分的面积.(计算结果精确到0.1)
(参考数值:π≈3.14, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是_____米,小明在书店停留了_____分钟;
(2)本次上学途中,小明一共行驶了______米,一共用了_____分钟;
(3)在整个上学的途中______(哪个时间段)小明骑车速度最快,最快的速度是____米/分;
(4)小明出发多长时间离家1200米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() +(﹣1)2017﹣(
+(﹣1)2017﹣(![]() ﹣
﹣![]() ),
),
(2)2(3a2b﹣2ab2)﹣3(ab2+2a2b),
(3)﹣7x2y﹣3xy2+5x2y+13xy,其中x=﹣![]() ,y=
,y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=72°30′,射线OC在∠AOB内,∠BOC=30°,
(1)∠AOC=_______;
(2)在图中画出∠AOC的一个余角,要求这个余角以O为顶点,以∠AOC的一边为边.图中你所画出的∠AOC的余角是______,这个余角的度数等于______.

查看答案和解析>>
科目:初中数学 来源: 题型:
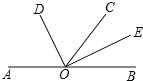
【题目】如图,点A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)当∠BOE=25°时,求∠AOD的度数
(2)在图中找出∠COD的补角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商店在某一时间以每件a元(a>0)的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%.
(1)当a=60时,分析卖出这两件衣服总的是盈利还是亏损,或是不盈不亏?
(2)小安发现:不论a为何值,这样卖两件衣服总的都是亏损.请判断“小安发现”是否正确?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠BOP与OP上点C,点A(在A的左侧),嘉嘉进行如下作图:
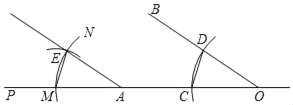
①以点O为圆心,OC为半径画弧,交OB于点D,连接CD
②以点A为圆心,OC为半径画弧MN,交AP于点M
③以点M为圆心,CD为半径画弧,交MN于点E,连接ME,作射线AE
如图所示,则下列结论不成立的是( )
A. CD∥EM B. AE∥OB C. ∠ODC=∠AEM D. ∠OAE=∠BDC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若 ![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com