
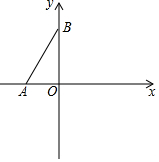
 如图,点O为平面直角坐标系的原点,点A在x轴上,点B在y轴上,且AO=2,∠ABO=30°.
如图,点O为平面直角坐标系的原点,点A在x轴上,点B在y轴上,且AO=2,∠ABO=30°.分析 (1)由AO=2、∠ABO=30°可得A(2,0),由BO=$\frac{AO}{tan∠ABO}$可得B(0,2$\sqrt{3}$);
(2)由旋转的性质得出OA=OA′=2、∠AOA′=60°、∠AOB=∠A′OB′=90°、OB=OB′=2$\sqrt{3}$,作A′C⊥x轴、B′D⊥x轴,解直角三角形即可得.
解答 解:(1)∵在Rt△ABO中,AO=2,∠ABO=30°,
∴BO=$\frac{AO}{tan∠ABO}$=$\frac{2}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$,
则点A(2,0)、B(0,2$\sqrt{3}$);
(2)由旋转可知OA=OA′=2,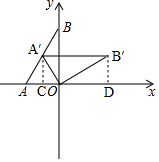
过点A′作A′C⊥x轴于点C,B′D⊥x轴于点D,
在Rt△A′OC中,A′C=OA′sin∠A′OC=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,CO=A′Ocos∠A′OC=2×$\frac{1}{2}$=1,
∴点A′(-1,$\sqrt{3}$),
∵∠AOA′=60°,∠AOB=∠A′OB′=90°,OB=OB′=2$\sqrt{3}$,
∴∠B′OD=30°,
在Rt△B′OD中,OD=OB′cos∠B′OD=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,B′D=OB′sin∠B′OD=2$\sqrt{3}$×$\frac{1}{2}$=$\sqrt{3}$,
∴点B′(3,$\sqrt{3}$).
点评 本题主要考查坐标与图形的性质,熟练掌握旋转的性质及解直角三角形的应用是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
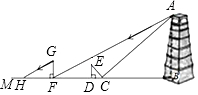 如图,小亮、小芳同学想测量一座塔的高度,他们经过观察发现需要两次测量,于是他们首先用平面镜进行测量,方法如下:如图,小芳在小亮和塔之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小亮看着镜面上的标记,来回走动,走到点D时,看到塔顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=3米;然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了17米,到达塔影子的末端F点处,此时,测得小亮身高GF的影长FH=4.2米,GF=1.6米,如图,已知AB⊥BM,ED⊥BM,GF⊥CM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中的信息,求出塔的高AB的长度.
如图,小亮、小芳同学想测量一座塔的高度,他们经过观察发现需要两次测量,于是他们首先用平面镜进行测量,方法如下:如图,小芳在小亮和塔之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小亮看着镜面上的标记,来回走动,走到点D时,看到塔顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=3米;然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:如图,小亮从D点沿DM方向走了17米,到达塔影子的末端F点处,此时,测得小亮身高GF的影长FH=4.2米,GF=1.6米,如图,已知AB⊥BM,ED⊥BM,GF⊥CM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中的信息,求出塔的高AB的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com