
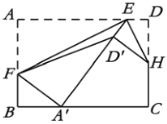
【题目】如图,矩形纸片![]() 中,
中,![]() ,
,![]() ,将纸片沿
,将纸片沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,折痕分别交边
处,折痕分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() .再将纸片沿
.再将纸片沿![]() 折叠,使点
折叠,使点![]() 落在线段
落在线段![]() 上的
上的![]() 处,折痕交边
处,折痕交边![]() 于点
于点![]() .连接
.连接![]() ,则
,则![]() 的长是______
的长是______![]() .
.
科目:初中数学 来源: 题型:
【题目】某自行车经销商计划投入7.1万元购进100辆A型和30辆B型自行车,其中B型车单价是A型车单价的6倍少60元.
(1)求A、B两种型号的自行车单价分别是多少元?
(2)后来由于该经销商资金紧张,投入购车的资金不超过5.86万元,但购进这批自行年的总数不变,那么至多能购进B型车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“美”、“丽”、“光”、“明”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“美”的概率;
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图或列表法,求甲取出的两个球上的汉字恰能组成“美丽”或“光明”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
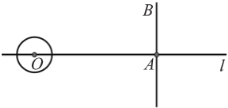
【题目】如图,在直线![]() 上有相距
上有相距![]() 的两点
的两点![]() 和
和![]() (点
(点![]() 在点
在点![]() 的右侧),以
的右侧),以![]() 为圆心作半径为
为圆心作半径为![]() 的圆,过点
的圆,过点![]() 作直线
作直线![]() .将
.将![]() 以
以![]() 的速度向右移动(点
的速度向右移动(点![]() 始终在直线
始终在直线![]() 上),则
上),则![]() 与直线
与直线![]() 在______秒时相切.
在______秒时相切.
A.3B.3.5C.3或4D.3或3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
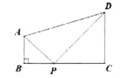
【题目】如图,四边形ABCD中,AB∥CD,∠B=90°,AB=1,CD=2,BC=3,点P为BC边上一动点,若△PAB与△PCD是相似三角形,则BP的长为 _____________
查看答案和解析>>
科目:初中数学 来源: 题型:
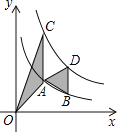
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小胖同学遇到这样一个问题,如图1,在△ABC中,∠ABC=45°,AB=2![]() ,AD=AE,∠DAE=90°,CE=
,AD=AE,∠DAE=90°,CE=![]() ,求CD的长;
,求CD的长;
小胖经过思考后,在CD上取点F使得∠DEF=∠ADB(如图2),进而得到∠EFD=45°,试图构建“一线三等角”图形解决问题,于是他继续分析,又意外发现△CEF∽△CDE.
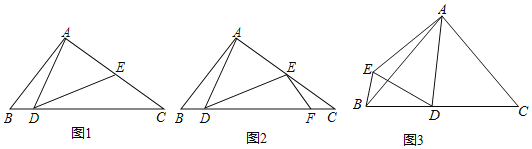
(1)请按照小胖的思路完成这个题目的解答过程.
(2)参考小胖的解题思路解决下面的问题:
如图3,在△ABC中,∠ACB=∠DAC=∠ABC,AD=AE,![]() ∠EAD+∠EBD=90°,求BE:ED.
∠EAD+∠EBD=90°,求BE:ED.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com