
【题目】如图,△ABC为等腰三角形,AB=AC,∠D=∠E,∠BAD=∠CAE.
(1)写出一对全等的三角形:△ ≌△ ;
(2)证明(1)中的结论;
(3)求证:点G为BC的中点.

科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(2k+1)x+k2+k(k>0)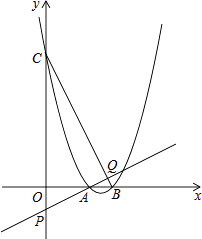
(1)当k= ![]() 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程x2﹣(2k+1)x+k2+k=0有两个不相等的实数根;
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
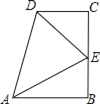
【题目】在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图.大家一起热烈地讨论交流,小英第一个得出如下结论:(1)AE平分∠DAB;(2)△EBA≌△DCE;(3)AB+CD=AD;(4)AE⊥DE;(5)AB∥CD.其中正确的结论是_____.(将你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:关于三角函数还有如下的公式:
sin(α±β)=sinαcosβ±cosαsinβ
tan(α±β)= ![]()
利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值.
例:tan75°=tan(45°+30°)= ![]() =
=  =2+
=2+ ![]()
根据以上阅读材料,请选择适当的公式解答下面问题
(1)计算:sin15°;
(2)某校在开展爱国主义教育活动中,来到烈士纪念碑前缅怀和纪念为国捐躯的红军战士.李三同学想用所学知识来测量如图纪念碑的高度.已知李三站在离纪念碑底7米的C处,在D点测得纪念碑碑顶的仰角为75°,DC为 ![]() 米,请你帮助李三求出纪念碑的高度.
米,请你帮助李三求出纪念碑的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1 , C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC= ![]() ,则AF的长度为( )
,则AF的长度为( ) 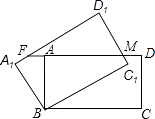
A.2﹣ ![]()
B.![]()
C.![]()
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形![]() 是半高三角形,且斜边
是半高三角形,且斜边![]() ,则它的周长等于_________.
,则它的周长等于_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁路上![]() 、
、![]() 两点相距25km,
两点相距25km,![]() 为良村庄,
为良村庄,![]() 于
于![]() ,
,![]() 于
于![]() ,已知
,已知![]() ,
,![]() ,现在要在铁路
,现在要在铁路![]() 上修建一个土特产收购站
上修建一个土特产收购站![]() .
.

(1)在图![]() 中,若
中,若![]() ,则
,则![]() 战应修建在离
战应修建在离![]() 站多少千米处.
站多少千米处.
(2)在图![]() 中,若
中,若![]() 值最小,则
值最小,则![]() 点应建在哪里,请求出这个最小值.
点应建在哪里,请求出这个最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com