
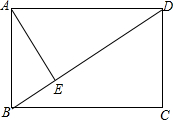
 已知:如图,矩形ABCD,AB长6cm,对角线BD比AD边大2cm,则AD的长为8cm,点A到BD的距离AE的长为4.8cm.
已知:如图,矩形ABCD,AB长6cm,对角线BD比AD边大2cm,则AD的长为8cm,点A到BD的距离AE的长为4.8cm. 分析 设AD=x,则BD=x+2,在Rt△ABD中,由AB2+AD2=BD2,推出62+x2=(x+2)2,推出x=8cm,推出AD=8cm,BD=10cm,由$\frac{1}{2}$•AB•AD=$\frac{1}{2}$•BD•AE,可得AE=$\frac{AB•AD}{BD}$由此即可解决问题.
解答 解:设AD=x,则BD=x+2,
在Rt△ABD中,∵AB2+AD2=BD2,
∴62+x2=(x+2)2,
∴x=8cm,
∴AD=8cm,BD=10cm,
∵$\frac{1}{2}$•AB•AD=$\frac{1}{2}$•BD•AE,
∴AE=$\frac{AB•AD}{BD}$=$\frac{6×8}{10}$=4.8cm.
故答案分别为8cm,4.8cm.
点评 本题考查矩形的性质、勾股定理、三角形的面积公式等知识,解题的关键是学会根据方程解决问题,学会利用面积法求直角三角形斜边上的高,属于中考常考题型.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:选择题
 将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上,则∠1和∠2的关系是( )
将两张长方形纸片如图所示摆放,使其中一张长方形纸片的一个顶点恰好落在另一张长方形纸片的一边上,则∠1和∠2的关系是( )| A. | ∠1=∠2 | B. | ∠1+∠2=90° | C. | ∠1+∠2=180° | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 初三某班学生去中央公园踏青,班级信息员骑自行车先从学校出发,5分钟后其余同学以60米/分的速度从学校向公园行进,信息员先到达公园后用5分钟找到聚集地点,再立即按原路以另一速度返回到队伍汇报聚集地点,最后与同学们一起步行到公园,信息员离其余同学的距离y(米)与信息员出发的时间x(分)之间的关系如图所示,则信息员开始返回之后,再经过3分钟与其余同学相距720米.
初三某班学生去中央公园踏青,班级信息员骑自行车先从学校出发,5分钟后其余同学以60米/分的速度从学校向公园行进,信息员先到达公园后用5分钟找到聚集地点,再立即按原路以另一速度返回到队伍汇报聚集地点,最后与同学们一起步行到公园,信息员离其余同学的距离y(米)与信息员出发的时间x(分)之间的关系如图所示,则信息员开始返回之后,再经过3分钟与其余同学相距720米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
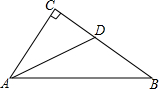 如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )
如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )| A. | 3 | B. | $\frac{15}{4}$ | C. | 5 | D. | $\frac{25}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
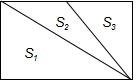 如图是由三个三角形组成的一个面积为(6a2+4a)cm2的长方形,三个三角形的面积分别是S1,S2,S3,若S1=(3a2+2a)cm2,S3=(2a2-a)cm2,则S2等于(a2+3a)cm2.
如图是由三个三角形组成的一个面积为(6a2+4a)cm2的长方形,三个三角形的面积分别是S1,S2,S3,若S1=(3a2+2a)cm2,S3=(2a2-a)cm2,则S2等于(a2+3a)cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com