
���� ��������һ�������ε�����x��y��z��������������֮�ʹ��ڵ����ߣ���������֮��С�ڵ����ߣ�
��� �⣺������x��y��z�������x+y��z��
��$\sqrt{x}$+$\sqrt{y}$��$\sqrt{x+y}$��$\sqrt{z}$���˽�����ȷ��
����x=3��y=4��z=5����x2��y2��z2�����������Σ��˽��۲���ȷ��
��$\frac{1}{2}$��x+y����$\frac{1}{2}$��x+z����$\frac{1}{2}$��y+z�����˽�����ȷ��
�ܣ�y-x��+��z-y����z-x����y-x+1��+��z-y+1����z-x+1���˽�����ȷ��
���Ԣ٢ۢ���ȷ��
�ʴ�Ϊ���٢ۢܣ�
���� ���⿼���������ε����߹�ϵ���Լ�������ֵ���뷨�Ƚ�һЩ���Ĵ�С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�콭��ʡ���꼶��ѧ�ڵ�һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ������
��ͼ����֪����ֱ������ABCD�У�AD��BC����C��90�㣬AB��AD��25��BC��32������BD��AE��BD������ΪE.
(1)��֤����ABE�ס�DBC��
(2)���߶�AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�콭��ʡ���꼶��ѧ�ڵ�һ��ģ�⿼����ѧ�Ծ��������棩 ���ͣ���ѡ��
����y=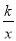 ��y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ� ��
��y=��kx2+k��k��0����ͬһֱ������ϵ�е�ͼ������ǣ� ��
A.  B.
B. 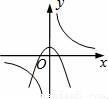 C.
C. 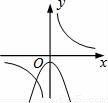 D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У���C������Ϊ��0��2��������A��ÿ��1����λ�����ٶȴӵ�O������x����������˶���M���߶�AC���е㣬���߶�AM�Ե�AΪ���ģ���˳ʱ�뷽����ת90��õ��߶�AB������CB�����ABC�����ΪS���˶�ʱ��Ϊt�룬������ͼ���У��ܱ�ʾS��t�ĺ�����ϵ��ͼ������ǣ�������
��ͼ����ƽ��ֱ������ϵ�У���C������Ϊ��0��2��������A��ÿ��1����λ�����ٶȴӵ�O������x����������˶���M���߶�AC���е㣬���߶�AM�Ե�AΪ���ģ���˳ʱ�뷽����ת90��õ��߶�AB������CB�����ABC�����ΪS���˶�ʱ��Ϊt�룬������ͼ���У��ܱ�ʾS��t�ĺ�����ϵ��ͼ������ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ��AD�ǡ�ABC��ƽ���ߣ���E��BC�ϣ���G��CA���ӳ����ϣ�EG��AB�ڵ�F����GE��AD����֤����AFG=��G��
��֪����ͼ��AD�ǡ�ABC��ƽ���ߣ���E��BC�ϣ���G��CA���ӳ����ϣ�EG��AB�ڵ�F����GE��AD����֤����AFG=��G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�ĶԽ��߽��ڵ�O����E���߶�0D��һ�㣬����EC����BF��CE�ڵ�F����0C�ڵ�G����AB=4��BF�ǡ�DBC�Ľ�ƽ���ߣ���OE�ij�Ϊ4-2$\sqrt{2}$��
��ͼ��������ABCD�ĶԽ��߽��ڵ�O����E���߶�0D��һ�㣬����EC����BF��CE�ڵ�F����0C�ڵ�G����AB=4��BF�ǡ�DBC�Ľ�ƽ���ߣ���OE�ij�Ϊ4-2$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 Сӱ�ü�����̽������ax2+bx+c=0�ĸ���������ͼ��ʾ��ͼ�����һ�����Ƹ�x=-3.4���̵���һ�����Ƹ�����ȷ��0.1��Ϊ��������
Сӱ�ü�����̽������ax2+bx+c=0�ĸ���������ͼ��ʾ��ͼ�����һ�����Ƹ�x=-3.4���̵���һ�����Ƹ�����ȷ��0.1��Ϊ��������| A�� | 4.4 | B�� | 3.4 | C�� | 2.4 | D�� | 1.4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ͼ���ڡ�ABC�У�AB=AC=10$\sqrt{2}$cm����BAC=45�㣬BD��AC��D����M�ӵ�A��������AC���������˶����ٶ�Ϊ2cm/s��ͬʱֱ��PQ�ɵ�B������BA���������˶����ٶ�Ϊ1cm/s���˶�������ʼ�ձ���PQ��AC��ֱ��PQ��AB��P����BC��Q����BD��F������PM�����˶�ʱ��Ϊt��s����0��t��5$\sqrt{2}$��������������⣺
��֪��ͼ���ڡ�ABC�У�AB=AC=10$\sqrt{2}$cm����BAC=45�㣬BD��AC��D����M�ӵ�A��������AC���������˶����ٶ�Ϊ2cm/s��ͬʱֱ��PQ�ɵ�B������BA���������˶����ٶ�Ϊ1cm/s���˶�������ʼ�ձ���PQ��AC��ֱ��PQ��AB��P����BC��Q����BD��F������PM�����˶�ʱ��Ϊt��s����0��t��5$\sqrt{2}$��������������⣺�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com