
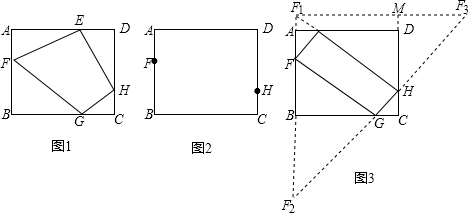
分析 探究1:如图1中,作F关于AD的对称点F′,F关于BC的对称点F″,连接HF′交AD于E,连接HF″交BC于G,作HM⊥AB于M.此时四边形EFGH的周长最小,最小值=EF+EH+GF+GH=EF′+EH+HG+GF″=HF′+HF″;
探究2:由题意可知四边形EFGH的周长的最小值=HF1+HF2,易知HF1是Rt△F1F2F3的斜边的中线,可得HF1=HF2=HF3,在Rt△F1F2F3中,F1F2=16,F1F3=12,
易知F2F3=$\sqrt{1{2}^{2}+1{6}^{2}}$=20,由此即可解决问题;
拓广探究:如图2中,当四边形EFGH的周长最小时,四边形EFGH是平行四边形,易知:CH:CG:GH=3:4:5,设HC=3x,GC=4x,GH=5x,则DH=6-3x,BG=8-4x,
DE=$\frac{4}{3}$(6-3x),AE=8-$\frac{4}{3}$(6-3x),BF=$\frac{3}{4}$(8-4x),AF=6-$\frac{3}{4}$(8-4x),构建二次函数即可解决问题;
解答 解:探究1:如图1中,作F关于AD的对称点F′,F关于BC的对称点F″,连接HF′交AD于E,连接HF″交BC于G,作HM⊥AB于M.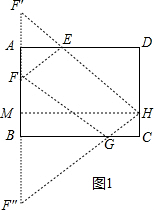
此时四边形EFGH的周长最小,最小值=EF+EH+GF+GH=EF′+EH+HG+GF″=HF′+HF″,
在Rt△HMF′中,HF′=$\sqrt{MF{′}^{2}+H{M}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
在Rt△HMF″中,HF″=$\sqrt{H{M}^{2}+F″{M}^{2}}$=$\sqrt{{8}^{2}+{5}^{2}}$=$\sqrt{89}$,
∴四边形EFGH的周长的最小值为10+$\sqrt{89}$;
探究2: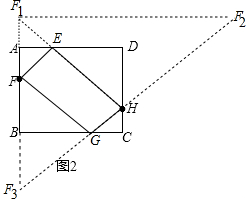
由题意可知四边形EFGH的周长的最小值=HF1+HF2,
易知HF1是Rt△F1F2F3的斜边的中线,
∴HF1=HF2=HF3,
在Rt△F1F2F3中,F1F2=16,F1F3=12,
∴F2F3=$\sqrt{1{2}^{2}+1{6}^{2}}$=20,
∴四边形EFGH的周长的最小值为20.
拓广探究:存在.理由如下:
如图2中,当四边形EFGH的周长最小时,四边形EFGH是平行四边形,易知:CH:CG:GH=3:4:5,设HC=3x,GC=4x,GH=5x,则DH=6-3x,BG=8-4x,
DE=$\frac{4}{3}$(6-3x),AE=8-$\frac{4}{3}$(6-3x),BF=$\frac{3}{4}$(8-4x),AF=6-$\frac{3}{4}$(8-4x),
∴S四边形EFGH=6×8-$\frac{1}{2}$•3x•4x-$\frac{1}{2}$•(6-3x)•$\frac{4}{3}$(6-3x)-$\frac{1}{2}$•[8-$\frac{4}{3}$(6-3x)]•[6-$\frac{3}{4}$(8-4x)]-$\frac{1}{2}$•(8-4x)•$\frac{3}{4}$(8-4x)
=-24x2+48x
=-24(x-1)2+24,
∵-24<0,
∴x=1时,四边形EFGH的面积最大,最大值为24.
点评 本题考查四边形综合题、轴对称的性质、勾股定理、二次函数等知识,解题的关键是灵活运用所学知识解决问题,学会构建二次函数解决最值问题,属于中考压轴题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:填空题
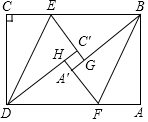 将一张矩形ABCD纸片,按如图进行折叠,分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE′与△A′BF,且边EC′的延长线与A′B交于点G,边FA的延长线与C′D交于一点H,已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=4,则线段BC=52.
将一张矩形ABCD纸片,按如图进行折叠,分别在BC,AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE′与△A′BF,且边EC′的延长线与A′B交于点G,边FA的延长线与C′D交于一点H,已知tan∠EBG=$\frac{3}{4}$,A′G=6,C′G=4,则线段BC=52.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )
如图,将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置,使点A,C,B′在同一条直线上,则旋转角的大小为( )| A. | 45° | B. | 90° | C. | 120° | D. | 135° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{7}{9}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com