
 小明要测量公园被湖水隔开的两棵大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°方向.
小明要测量公园被湖水隔开的两棵大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°方向.分析 (1)先利用平行线的性质得∠ACM=∠DAC=15°,再利用平角的定义计算出∠ACB=105°,然后根据三角形内角和计算∠ABC的度数;
(2)作CH⊥AB于H,如图,易得△ACH为等腰直角三角形,则AH=CH=$\frac{\sqrt{2}}{2}$AC=100$\sqrt{2}$,在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=$\sqrt{3}$CH=100$\sqrt{6}$,AB=AH+BH=100$\sqrt{2}$+100$\sqrt{6}$,然后进行近似计算即可.
解答 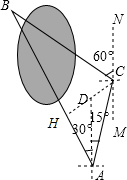 解:(1)∵CM∥AD,
解:(1)∵CM∥AD,
∴∠ACM=∠DAC=15°,
∴∠ACB=180°-∠BCN-∠ACM=180°-60°-15°=105°,
而∠BAC=30°+15°=45°,
∴∠ABC=180°-45°-105°=30°;
(2)作CH⊥AB于H,如图,
∵∠BAC=45°,
∴△ACH为等腰直角三角形,
∴AH=CH=$\frac{\sqrt{2}}{2}$AC=$\frac{\sqrt{2}}{2}$×200=100$\sqrt{2}$,
在Rt△BCH中,∵∠HBC=30°,
∴BH=$\sqrt{3}$CH=100$\sqrt{6}$,
∴AB=AH+BH=100$\sqrt{2}$+100$\sqrt{6}$≈141.4+244.9≈386.
答:两棵大树A和B之间的距离约为386米.
点评 本题考查了解直角三角形的应用-方向角问题:在解决有关方向角的问题中,一般要根据题意理清图形中各角的关系,有时所给的方向角并不一定在直角三角形中,需要用到两直线平行内错角相等或一个角的余角等知识转化为所需要的角.解决此题的关键作CH⊥AB构建含特殊角的直角三角形.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:填空题
 在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.
在猜一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图的五张卡片中任意拿走三张,使剩下的卡片从左到右连成一个两位数,该数就是他猜的价格.如果商品的价格是50元,那么他一次就能猜中的概率是$\frac{1}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=4,那么点B与C′的距离为( )
如图,AD为△ABC的BC边上的中线,沿AD将△ACD折叠,C的对应点为C′,已知∠ADC=45°,BC=4,那么点B与C′的距离为( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com