
【题目】某商场销售A、B两种型号的电风扇,进价及售价如表:
品牌 | A | B |
进价(元/台) | 120 | 180 |
售价(元/台) | 150 | 240 |
(1)该商场4月份用21000元购进A、B两种型号的电风扇,全部售完后获利6000元,求商场4月份购进A、B两种型号电风扇的数量;
(2)该商场5月份计划用不超过42000元购进A、B两种型号电风扇共300台,且B种型号的电风扇不少于50台;销售时准备A种型号的电风扇价格不变,B种型号的电风扇打9折销售.那么商场如何进货才能使利润最大?
【答案】(1)商场4月份购进A种型号的电风扇100台,B种型号的电风扇50台;(2)A种型号的电风扇购进200台,B种型号的电风扇购进100台时,利润最大.
【解析】
(1)设4月份购进A种型号的电风扇x台,B种型号的电风扇y台,根据购买费用和获利分别可列写一个关于x、y的方程,求解可得;
(2)设5月份购进A种型号的电风扇m台,利润为w元,根据题意得出w关于m的一次函数,然后再根据m的取值范围确定最大值情况.
(1)设4月份购进A种型号的电风扇x台,B种型号的电风扇y台,
依题意得: ,解得:
,解得:![]() .
.
答:商场4月份购进A种型号的电风扇100台,B种型号的电风扇50台.
(2)设5月份购进A种型号的电风扇m台,则购进B种型号的电风扇(300﹣m)台,利润为w元.
由题意得,120m+180(300﹣m)≤42000,
解不等式得:m≥200,
又∵300﹣m≥50,即m≤250,
∴200≤m≤250,
w=(150﹣120)m+(0.9×240﹣180)(300﹣m)=﹣6m+10800,
∵﹣6<0,w随m的增大而减小,
∴当m=200时,w有最大值,此时,300﹣m=100.
答:A种型号的电风扇购进200台,B种型号的电风扇购进100台时,利润最大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 、
、![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,
轴上,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一动点,以
上一动点,以![]() 为边在
为边在![]() 轴上方作正方形
轴上方作正方形![]() ,连接
,连接![]() .
.

(1)若点![]() 的坐标为
的坐标为![]() ,则
,则![]() ________;
________;
(2)当![]() ________时,
________时,![]() 轴;
轴;
(3)当点![]() 由点
由点![]() 运动到点
运动到点![]() 过程中,点
过程中,点![]() 经过的路径长为________;
经过的路径长为________;
(4)当![]() 面积最大时,求出
面积最大时,求出![]() 的长及
的长及![]() 面积最大值.
面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
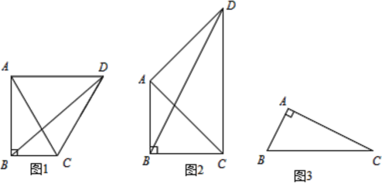
(1)如图1,在Rt△ABC中,∠BAC=30°,∠ABC=90°,将线段AC绕点A逆时针旋转,旋转角α=2∠BAC, ∠BCD的度数是 ;线段BD,AC之间的数量关系是 .
类比探究:
(2)在Rt△ABC中,∠BAC=45°,∠ABC=90°,将线段AC绕点A逆时针旋转,旋转角α=2∠BAC,请问(1)中的结论还成立吗?;
拓展延伸:
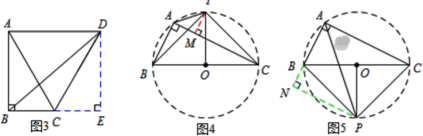
(3)如图3,在Rt△ABC中,AB=2,AC=4,∠BDC=90°,若点P满足PB=PC,∠BPC=90°,请直接写出线段AP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
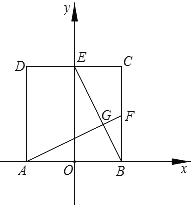
【题目】如图,在正方形ABCD中,顶点A(﹣1,0),C(1,2),点F是BC的中点,CD与y轴交于点E,AF与BE交于点G.将正方形ABCD绕点O顺时针旋转,每次旋转90°,则第99次旋转结束时,点G的坐标为( )
A.(![]() ,
,![]() )B.(﹣
)B.(﹣![]() ,
,![]() )C.(﹣
)C.(﹣![]() ,
,![]() )D.(
)D.(![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
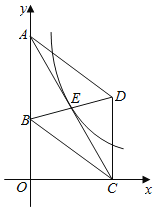
【题目】如图,在平面直角坐标系中,平行四边形ABCD的边AB在y轴上,点D(4,4),cos∠BCD=![]() ,若反比例函数y=
,若反比例函数y=![]() (k≠0)的图象经过平行四边形对角线的交点E,则k的值为( )
(k≠0)的图象经过平行四边形对角线的交点E,则k的值为( )
A.14B.7C.8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
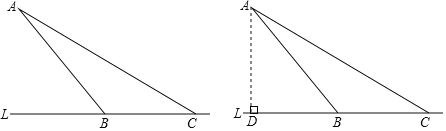
【题目】根据道路交通法规规定:普通桥梁一般限速40km/h.为了安全,交通部门在桥头竖立警示牌:“请勿超速”,并监测摄像系统监控,如图,在某直线公路L路桥段BC内限速40km/h,为了检测车辆是否超速,在距离公路L500米旁的A处设立了观测点,从观测点A测得一小车从点B到达点C行驶了30秒钟,已知∠ABL=45°,∠ACL=30°,此车超速了吗?请说明理由.(参考数据:![]() =1.41,
=1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现
小明在学习鲁教版八年级上册97页例4时,受到启发进行如下数学实验操作:
如图1,取一个锐角为45°的三角尺,把锐角顶点放在正方形ABCD的顶点D处,将三角尺绕点D旋转一个角度,使三角尺的直角边与斜边分别交边AB,BC于点E和点F,连接FE,在绕点D旋转过程中,发现线段AE,EF,CF满足EF=AE+CF的数量关系,但是不会进行证明,数学张老师给他如下的提示:把△ADE绕点D逆时针旋转90°至△DCE’的位置,小明画旋转后的图形,利用全等的知识证明了出来.你根据上面的提示画出旋转后的图形,并将上面的结论进行证明.



问题探究
小明的探究引发了老师的兴趣,老师将三角尺绕点D旋转到如图2的位置,三角尺的直角边与斜边分别交边AB,BC的延长线于点E和点F,老师问题小明此时AE,EF,CF满足什么数量关系,小明思考后说出了正确的结论.请同学们直接写出正确结论(不用写出证明过程).
拓展延伸
张老师让小明利用上面探究积累的学习经验,解答下面的问题:
如图3已知正方形ABCD,点E在边AB上,点F在边BC上,且∠EDF=45°,若CD=6,AE=2,求CF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com