
【题目】如图,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,∠AEO=∠C,OE交BC于点F.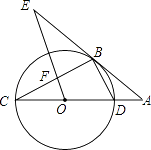
(1)求证:OE∥BD;
(2)当⊙O的半径为5,sin∠DBA= ![]() 时,求EF的长.
时,求EF的长.
【答案】
(1)证明:连接OB,
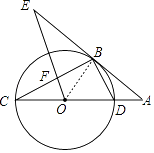
∵CD为⊙O的直径,
∴∠CBD=∠CBO+∠OBD=90°,
∵AE是⊙O的切线,
∴∠ABO=∠OBD+∠ABD=90°,
∴∠ABD=∠CBO,
∵OB、OC是⊙O的半径,
∴OB=OC.
∴∠C=∠CBO,
∴∠C=∠ABD,
∵∠E=∠C,
∴∠E=∠ABD,
∴OE∥BD
(2)解:由(1)可得sin∠C=∠DBA= ![]() ,
,
在Rt△OBE中,sin∠C= ![]() ,OC=5
,OC=5
∴BD=4,
∵∠CBD=∠EBO=90°,∠E=∠C,
∴△CBD∽△EBO.
∴ ![]() =
= ![]() ,
,
∴EO= ![]() ,
,
∵OE∥BD,CO=OD,
OF= ![]() BD=2,
BD=2,
∴CF=FB.
EF=OE﹣OF= ![]()
【解析】(1) 连接OB,由直径所对的圆周角是直角得出∠CBD=∠CBO+∠OBD=90°,又由切线的性质定理得出∠ABO=∠OBD+∠ABD=90°,进而得出∠ABD=∠CBO,由同圆的半径相等得出∠C=∠CBO,进而得出∠C=∠ABD,∠E=∠ABD,由平行线的判断定理得出结论;(2)由(1)可得sin∠C=∠DBA在在Rt△OBE中根据sin∠C得出BD的长度,进而判断出△CBD∽△EBO.由相似三角形的性质得出OE的长度,最后由中位线的判断得出CF=FB.进而得出结论。
【考点精析】本题主要考查了平行线的判定和圆周角定理的相关知识点,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )
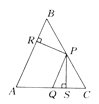
A. ①③ B. ②③ C. ①② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
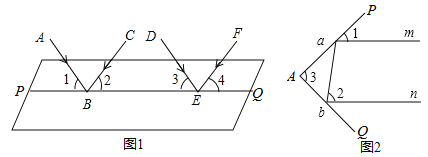
【题目】科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图1,一束平行光线![]() 与
与![]() 射向一个水平镜面后被反射,此时有
射向一个水平镜面后被反射,此时有![]() ,
,![]() .如图2,一束光线
.如图2,一束光线![]() 射到平面镜
射到平面镜![]() 上,被平面镜
上,被平面镜![]() 反射到平面镜
反射到平面镜![]() 上,又被
上,又被![]() 镜反射,若平面镜
镜反射,若平面镜![]() 反射出的光线
反射出的光线![]() 平行于光线
平行于光线![]() .
.
(1)当![]() ,求
,求![]() 的度数;
的度数;
(2)求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
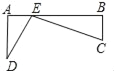
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在直线l上,点Q沿着直线l以3厘米/秒的速度由点A向右运动,以AQ为边作Rt△ABQ,使∠BAQ=90°,tan∠ABQ= ![]() ,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过△ABQ的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF=
,点C在点Q右侧,CQ=1厘米,过点C作直线m⊥l,过△ABQ的外接圆圆心O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF= ![]() CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.
CD,以DE、DF为邻边作矩形DEGF.设运动时间为t秒.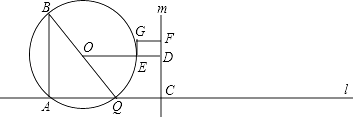
(1)直接用含t的代数式表示BQ、DF;
(2)当0<t<1时,求矩形DEGF的最大面积;
(3)点Q在整个运动过程中,当矩形DEGF为正方形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax﹣1的图象与反比例函数y= ![]() 的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.
的图象交于A(3,1),B两点,与x轴交于点C,与y轴交于点D.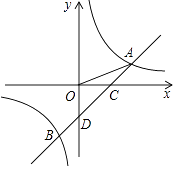
(1)求a,k的值及点B的坐标;
(2)直接写出不等式ax﹣1≥ ![]() 的解集;
的解集;
(3)在x轴上存在一点P,使得△POA与△OAC相似(不包括全等),请你求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列证明:
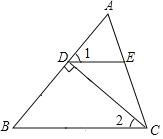
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知),
∴∠1+ =90°( ).
∵∠1+∠2=90°(已知),
∴ =∠2( ).
∴DE∥BC( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实数范围内定义一种运算“*”,其运算法则为a*b=a2﹣ab.根据这个法则,下列结论中正确的是_______.(把所有正确结论的序号都填在横线上)
①![]() *
*![]() =2﹣
=2﹣![]() ;②若a+b=0,则a*b=b*a;③(x+2)*(x+1)=0是一元二次方程;④方程(x+3)*1=1的根是x1=
;②若a+b=0,则a*b=b*a;③(x+2)*(x+1)=0是一元二次方程;④方程(x+3)*1=1的根是x1=![]() ,x2=
,x2=![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com