
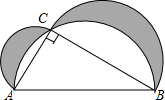
 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,分别以AC、BC、AB为直径作半圆,求图中阴影部分的面积.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,分别以AC、BC、AB为直径作半圆,求图中阴影部分的面积. 分析 先利用勾股定理列式求出BC,再根据阴影部分面积等于以AC、BC为直径的两个半圆的面积加上直角三角形ABC的面积减去以AB为直径的半圆的面积,列式计算即可得解.
解答 解:∵在Rt△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,
∵AB=5,AC=3,
∴BC=$\sqrt{{5}^{2}-{3}^{2}}$=4.
S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC-直径为AB的半圆的面积
=$\frac{1}{2}$π($\frac{AC}{2}$)2+$\frac{1}{2}$π($\frac{BC}{2}$)2+$\frac{1}{2}$AC×BC-$\frac{1}{2}$π($\frac{AB}{2}$)2
=$\frac{1}{8}$π(AC)2+$\frac{1}{8}$π(BC)2-$\frac{1}{8}$π(AB)2+$\frac{1}{2}$AC×BC
=$\frac{1}{8}$π(AC2+BC2-AB2)+$\frac{1}{2}$AC×BC
=$\frac{1}{2}$AC×BC
=$\frac{1}{2}$×3×4
=6.
点评 本题考查了勾股定理,半圆的面积,熟记定理并观察图形表示出阴影部分的面积是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E,F分别在矩形ABCD的边BC,AD上,EF∥AB,AB=6,AD=8,当AF=$\frac{9}{2}$时,矩形ABEF与矩形ADCB相似.
如图,点E,F分别在矩形ABCD的边BC,AD上,EF∥AB,AB=6,AD=8,当AF=$\frac{9}{2}$时,矩形ABEF与矩形ADCB相似.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 时间/min | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| 人数 | 1 | 2 | 5 | 15 | 10 | 5 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com