
【题目】如图1,在平面直角坐标系中,直线![]() 分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形(有一个角是直角的平行四边形).
分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形(有一个角是直角的平行四边形).
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作PHOA,垂足为H,连接NP.设点P的运动时间为t秒.
①若△NPH的面积为1,求t的值;
②点Q是点B关于点A的对称点,问BPPHHQ是否有最小值,如果有,直接写出相应的点P的坐标;如果没有,请说明理由.
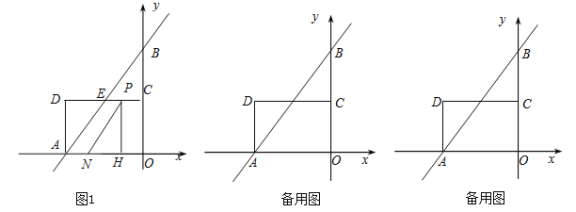
【答案】(1)A(﹣3,0),B(0,4),E(﹣1.5,2);(2)①t=1或2;(2)P(﹣2,2).
【解析】
(1)分别令x与y等于0,即可求出点A与点B的坐标,由四边形AOCD为矩形,可知:CD∥x轴,进而可知:D、C、E三点的纵坐标相同,由点C为OB的中点,可求点C的坐标,然后将点C的纵坐标代入直线y=![]() x+4即可求直线AB与CD交点E的坐标;
x+4即可求直线AB与CD交点E的坐标;
(2)①分两种情况讨论,第一种情况:当0<t<2时;第二种情况:当2<t≤6时;
②由点Q是点B关于点A的对称点,先求出点Q的坐标,然后连接PB,CH,可得四边形PHCB是平行四边形,进而可得:PB=CH,进而可将BP+PH+HQ转化为CH+HQ+2,然后根据两点之间线段最短可知:当点C,H,Q在同一直线上时,CH+HQ的值最小,然后求出直线CQ的关系式,进而可求出直线CQ与x轴的交点H的坐标,从而即可求出点P的坐标
(1)∵直线y=![]() x+4分别交x轴,y轴于A,B两点,
x+4分别交x轴,y轴于A,B两点,
∴令x=0得:y=4,
令y=0得:x=-3,
∴A(-3,0),B(0,4),
∴OA=3,OB=4,
∵点C为OB的中点,
∴OC=2,
∴C(0,2),
∵四边形AOCD为矩形,
∴OA=CD=3,OC=AD=2,CD∥OA(x轴),
∴D、C、E三点的纵坐标相同,
∴点E的纵坐标为2,将y=2代入直线y=![]() x+4得:x=-1.5,
x+4得:x=-1.5,
∴E(-1.5,2);
(2)①分两种情况讨论:
第一种情况当0≤t<1.5时,如图1,
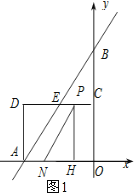
根据题意可知:经过t秒,CP=t,AN=t,HO=CP=t,PH=OC=2,
∴NH=3-2t,
∵S△NPH=![]() PHNH,且△NPH的面积为1,
PHNH,且△NPH的面积为1,
∴![]() ×2×(3-2t)=1,
×2×(3-2t)=1,
解得:t=1;
第二种情况:当1.5≤t≤3时,如图2,
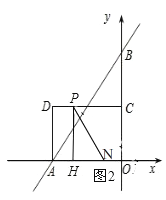
根据题意可知:经过t秒,CP=t,AN=t,HO=CP=t,PH=OC=2,
∴AH=3-t,
∴HN=AN-AH=t-(3-t)=2t-3,
∵S△NPH=![]() PHNH,且△NPH的面积为1,
PHNH,且△NPH的面积为1,
∴![]() ×2×(2t-3)=1,
×2×(2t-3)=1,
解得:t=2;
∴当t=1或2时,存在△NPH的面积为1;
②BP+PH+HQ有最小值,
连接PB,CH,HQ,则四边形PHCB是平行四边形,如图3,
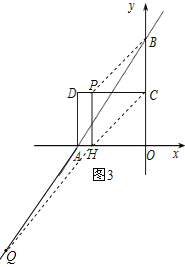
∵四边形PHCB是平行四边形,
∴PB=CH,
∴BP+PH+HQ=CH+HQ+2,
∵BP+PH+HQ有最小值,即CH+HQ+2有最小值,
∴只需CH+HQ最小即可,
∵两点之间线段最短,
∴当点C,H,Q在同一直线上时,CH+HQ的值最小,
过点Q作QM⊥y轴,垂足为M,
∵点Q是点B关于点A的对称点,
∴OA是△BQM的中位线,
∴QM=2OA=6,OM=OB=4,
∴Q(-6,-4),
设直线CQ的关系式为:y=kx+b,
将C(0,2)和Q(-6,-4)分别代入上式得:
![]() ,
,
解得:![]() ,
,
∴直线CQ的关系式为:y=x+2,
令y=0得:x=-2,
∴H(-2,0),
∵PH∥y轴,
∴P(-2,2).


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】在“双十二”期间,A,B两个超市开展促销活动,活动方式如下:
A超市:购物金额打9折后,若超过2000元再优惠300元;
B超市:购物金额打8折.
某学校计划购买某品牌的篮球做奖品,该品牌的篮球在A,B两个超市的标价相同.根据商场的活动方式:
(1)若一次性付款4200元购买这种篮球,则在B商场购买的数量比在A商场购买的数量多5个.请求出这种篮球的标价;
(2)学校计划购买100个篮球,请你设计一个购买方案,使所需的费用最少.(直接写出方案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若从中任取一球(不放回),再从中任取一球,请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率.
(3)若设计一种游戏方案:从中任取两球,两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A城气象台测得台风中心在A城正西方向600km的B处,以每小时200km的速度向北偏东60°的方向移动,距台风中心500km的范围内是受台风影响的区域.

(1)A城是否受到这次台风的影响?为什么?
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响有多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
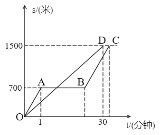
【题目】“龟兔赛跑”的故事同学们都听过,图中的线段OD和折线OABC表示龟兔赛跑时路程与时间的关系,请根据图中的信息,解决下列问题:
(1)填空:折线OABC表示赛跑过程中_________(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全程是_______米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后以400米/分钟的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中真命题的个数是( )
①平面内,过一点有且只有一条直线与已知直线平行;②![]() 这5个数中有2个是无理数;③若
这5个数中有2个是无理数;③若![]() ,则点P(-m,5)在第一象限;④
,则点P(-m,5)在第一象限;④![]() 的算术平方根是4;⑤经过一点有且只有一条直线与已知直线垂直;⑥同旁内角互补.
的算术平方根是4;⑤经过一点有且只有一条直线与已知直线垂直;⑥同旁内角互补.
A.2B.3C.4D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com