
【题目】(1)问题发现:
如图①,△ABC 和△AED 都是等腰直角三角形,∠BAC=∠EAD=90°,点 B 在线段AE 上,点 C 在线段AD 上,请直接写出线段 BE 与线段 CD 的数量与位置关系是关系: ;
(2)操作探究:
如图②,将图①中的△ABC 绕点 A 顺时针旋转α(0°<α<360°),(1)小题中线段 BE 与线段 CD 的关系是否成立?如果不成立,说明理由,如果成立,请你结合图②给出的情形进行证明;
(3)解决问题:
将图①中的△ABC 绕点 A 顺时针旋转α(0°<α<360°),若 DE=2AC,在旋转的过程中,当以 A、B、C、D 四点为顶点的四边形是平行四边形时,在备用图中画出其中的一个情形,并写出此时旋转角α的度数是 度.

【答案】(1)BE=CD,BE⊥CD(2)成立(3)45°或 225°或 315°
【解析】
(1)根据等腰直角三角形的性质可得AB=AC,AE=AD,再根据等量关系可得线段BE与线段CD的关系;
(2)根据等腰直角三角形的性质可得AB=AC,AE=AD,根据旋转的性质可得∠BAE=∠CAD,根据SAS可证△BAE≌△CAD,根据全等三角形的性质即可求解;
(3)根据平行四边形的性质可得∠ABC=∠ADC=45°,再根据等腰直角三角形的性质即可求解.
(1)∵△ABC 和△AED 都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,BE⊥CD,
∴AE﹣AB=AD﹣AC,
∴BE=CD;
故答案为:BE=CD,BE⊥CD;
(2)(1)结论成立,
理由:如图,
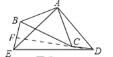
∵△ABC 和△AED 都是等腰直角三角形,∠BAC=∠EAD=90°,
∴AB=AC,AE=AD,
由旋转的性质得,∠BAE=∠CAD,
在△BAE 与△CAD 中, ,
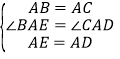 ,
,
∴△BAE≌△CAD(SAS)
∴BE=CD;∠AEB=∠ADC,
∴∠BED+∠EDF=∠AED+∠AEB+∠EDF=∠AED+∠ADC+∠EDF=∠AED+∠ADE=90°,
∴EFD=90°, 即:BE⊥CD
(3)如图,
∵以 A、B、C、D 四点为顶点的四边形是平行四边形,△ABC 和△AED 都是等腰直角三角形,
∴∠ABC=∠ADC=45°,
∵ED=2AC,
∴AC=CD,
∴∠CAD=45°
或360°﹣90°﹣45°=225°,或 360°﹣45°=315°
∴角α的度数是 45°或 225°或 315°.
故答案为:45°或 225°或 315(其中一种情况就可以).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影. 甲同学的方案公平吗?请用列表或画树状图的方法说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,先对折矩形得折痕MN,再折纸使折线过点B,且使得A在MN上,这时折线EB与BC所成的角为( )
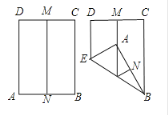
A.30°B.45°C.60°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,E为边上一点,连结AE并延长交直线DC于F,且CE=CF.
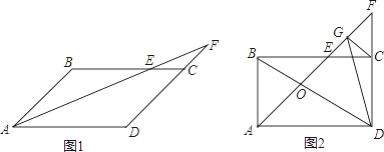
(1)如图1,求证:AF是∠BAD的平分线;
(2)如图2,若∠ABC=90°,点G是线段EF上一点,连接DG、BD、CG,若∠BDG=45°,求证:CG=![]() EF.
EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】附加题:(1)已知:如图①,在![]() 和
和![]() 中,OA=OB,OC=OD,
中,OA=OB,OC=OD,![]() ,求证:①AC=BD;②
,求证:①AC=BD;②![]() .
.
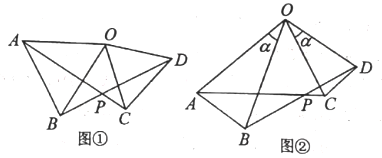
(2)如图②,在![]() 和
和![]() 中,若OA=OB,OC=OD,
中,若OA=OB,OC=OD,![]() ,则AC与BD间的等量关系式为 ;
,则AC与BD间的等量关系式为 ;![]() 的大小为 .
的大小为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题用适当的方法解下列方程
(1)(3x﹣1)(4x+5)=0
(2)4x2﹣8x﹣3=0(配方法)
(3)x(x+1)=3x+6
(4)(x﹣2)(x+4)=16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝新中国成立70周年,某校组织八年级全体学生参加“恰同学少年,忆峥嵘岁月”新中国成立70周年知识竞赛活动.将随机抽取的部分学生成绩进行整理后分成5组,50~60分(![]() )的小组称为“学童”组,60~70分(
)的小组称为“学童”组,60~70分(![]() )的小组称为“秀才”组,70~80分(
)的小组称为“秀才”组,70~80分(![]() )的小组称为“举人”组,80~90分(
)的小组称为“举人”组,80~90分(![]() )的小组称为“进士”组,90~100分(
)的小组称为“进士”组,90~100分(![]() )的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
)的小组称为“翰林”组,并绘制了不完整的频数分布直方图如下,请结合提供的信息解答下列问题:
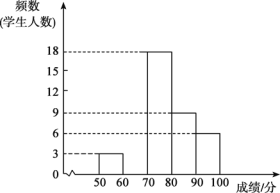
(1)若“翰林”组成绩的频率是12.5%,请补全频数分布直方图;
(2)在此次比赛中,抽取学生的成绩的中位数在 组;
(3)学校决定对成绩在70~100分(![]() )的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
)的学生进行奖励,若八年级共有336名学生,请通过计算说明,大约有多少名学生获奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与○O相交于点D,连接BD,则∠DBC的大小为

A. 15° B. 35° C. 25° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是
A. 连续抛一均匀硬币2次必有1次正面朝上
B. 连续抛一均匀硬币10次都可能正面朝上
C. 大量反复抛一均匀硬币,平均100次出现正面朝上50次
D. 通过抛一均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com