【题目】如图，在Rt△ABC中，∠B=90°，AB=3，BC=4，将△ABC折叠，使点B恰好落在边AC上，与点B′重合，AE为折痕，则EB′= ．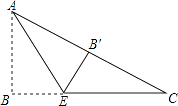 
津桥教育计算小状元系列答案科目：初中数学 来源： 题型：
【题目】任何一个正整数n都可以进行这样的分解：n＝s×t(s，t是正整数，且s≤t)，如果p×q在n的所有这种分解中两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：
、例如18可以分解成1×18，2×9，3×6这三种，这时就有
．给出下列关于F(n)的说法：(1)
；(2)
；(3)F(27)＝3；(4)若n是一个整数的平方，则F(n)＝1．其中正确说法的有_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们用
表示不大于
的最大整数，例如：
，
，
；用
表示大于的最小整数，例如：
，
，
.解决下列问题：
（1）
= ,，
= ；
（2）若
=2，则
的取值范围是 ；若
=－1，则
的取值范围是 ；
（3）已知，满足方程组
，求，的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）问题背景：已知，如图1，等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，AB=a，△ABC的面积为S，则有BC=
a，S=
a2．
（2）迁移应用：如图2，△ABC和△ADE都是等腰三角形，∠BAC=∠DAE=120°，D，E，C三点在同一条直线上，连接BD．
①求证：△ADB≌△AEC；
②求∠ADB的度数．
③若AD=2，BD=4，求△ABC的面积．
（3）拓展延伸：如图3，在等腰△ABC中，∠BAC=120°，在∠BAC内作射线AM，点D与点B关于射线AM轴对称，连接CD并延长交AM于点E，AF⊥CD于F，连接AD，BE．
①求∠EAF的度数；
②若CD=5，BD=2，求BC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将正整数1至2019按一定规律排列如下表：
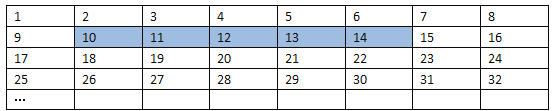
平移表中带阴影的方框，则方框中五个数的和可以是（ ）
A. 2010 B. 2018 C. 2019 D. 2020
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学校开展“文明礼仪”演讲比赛，八(1)班、八(2)班派出的5名选手的比赛成绩如图所示．
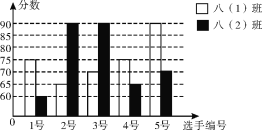
（1）根据上图，完成表格.
平均数 | 中位数 | 方差 | |
八(1)班 | 75 | _______ | _______ |
八(2)班 | 75 | 70 | 160 |
（2）结合两班选手成绩的平均数和方差，分析两个班级参加比赛的选手的成绩．
（3）如果在每班参加比赛的选手中分别选出3人参加决赛，从平均分看，你认为哪个班的实力更强一些？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在我市举行的中学生安全知识竞赛中共有20道题．每一题答对得5分，答错或不答都扣3分．
（1）小李考了60分，那么小李答对了多少道题？
（2）小王获得二等奖（75～85分），请你算算小王答对了几道题？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y=﹣x+2的图象与反比例函数y=﹣ 
的图象交于A、B两点，与x轴交于D点，且C、D两点关于y轴对称．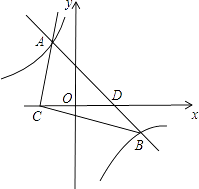 
（1）求A、B两点的坐标；
（2）求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
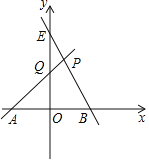
【题目】如图，已知直线AQ与x轴负半轴交于点A，与y轴正半轴交于点Q，∠QAO=45°，直线AQ在y轴上的截距为2，直线BE：y=-2x+8与直线AQ交于点P．
（1）求直线AQ的解析式；
（2）在y轴正半轴上取一点F，当四边形BPFO是梯形时，求点F的坐标．
（3）若点C在y轴负半轴上，点M在直线PA上，点N在直线PB上，是否存在以Q、C、M、N为顶点的四边形是菱形，若存在请求出点C的坐标；若不存在请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
