
分析 设直角三角形的两直角边长分别为a、b,再由直角三角形的斜边上的中线长为3得出斜边长为6,根据三角形的面积公式及勾股定理求出a+b的值,进而可得出结论.
解答 解:设直角三角形的两直角边长分别为a、b,
∵直角三角形的斜边上的中线长为3,
∴斜边长为6.
∵面积为2,
∴$\left\{\begin{array}{l}{\frac{1}{2}ab=2①}\\{{a}^{2}+{b}^{2}=36②}\end{array}\right.$,
由①得,2ab=8③,
②+③得,(a+b)2=44,
∴a+b=2$\sqrt{11}$,
∴这个直角三角形的周长=a+b+6=2$\sqrt{11}$+6.
故答案为:2$\sqrt{11}$+6.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.


科目:初中数学 来源: 题型:解答题
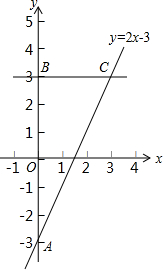 在平面直角坐标系xOy中,直线y=2x-3与y轴交于点A,点A与点B关于x轴对称,过点B作y轴的垂线l,直线l与直线y=2x-3交于点C.
在平面直角坐标系xOy中,直线y=2x-3与y轴交于点A,点A与点B关于x轴对称,过点B作y轴的垂线l,直线l与直线y=2x-3交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
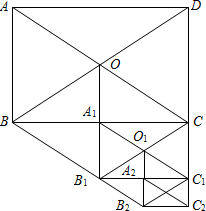 如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积为( )
如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积为( )| A. | 6 | B. | 3.75 | C. | 15 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}{3(x+1)<2x+3}\\{\frac{x-1}{3}≤\frac{2}{x}}\end{array}\right.$,并在数轴上表示它们的解集.
解不等式组$\left\{\begin{array}{l}{3(x+1)<2x+3}\\{\frac{x-1}{3}≤\frac{2}{x}}\end{array}\right.$,并在数轴上表示它们的解集.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com