
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.

(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6![]() ,AF=4
,AF=4![]() ,求AE的长.
,求AE的长.
【答案】(1)见解析;(2)6.
【解析】
试题分析:(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC;
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在Rt△ADE中,利用勾股定理求出线段AE的长度.
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
在△ADF与△DEC中,
![]()
∴△ADF∽△DEC.
(2)解:∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴![]() ,∴DE=
,∴DE=![]() =
=![]() =12.
=12.
在Rt△ADE中,由勾股定理得:AE=![]() =
=![]() =6.
=6.


科目:初中数学 来源: 题型:
【题目】如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).当△ADE的一边与△ABC的某一边平行(不共线)时,写出旋转角α的所有可能的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
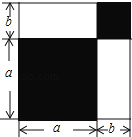
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动.在运动过程中,当△APC为等腰三角形时,点P出发的时刻t可能的值为( )

A.5 B.5或8 C.![]() D.4或
D.4或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据:![]() ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com