
【题目】如图,直线![]() 与x轴交于点A(3,0),与y轴交于点B,抛物线
与x轴交于点A(3,0),与y轴交于点B,抛物线![]() 经过A,B.
经过A,B.
(1)求抛物线解析式;
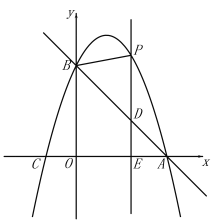
(2)E(m,0)是x轴上一动点,过点E作![]() 轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
轴于点E,交直线AB于点D,交抛物线于点P,连接PB.
①点E在线段OA上运动,若△PBD是等腰三角形时,求点E的坐标;
②点E在x轴的正半轴上运动,若![]() ,请直接写出m的值.
,请直接写出m的值.
【答案】(1)![]() ;(2)①点E的坐标为
;(2)①点E的坐标为![]() ,
,![]() 或
或![]() ;②m的值为
;②m的值为![]() 或5
或5
【解析】
(1)把![]() 代入
代入![]() ,求出点B的坐标,再把
,求出点B的坐标,再把![]() 代入
代入![]() ,求出b,c的值即可;
,求出b,c的值即可;
(2)先求出![]() ,①分
,①分![]() ,
,![]() ,
,![]() 三种情况分析即可;②先求出直线BC的解析式,当点P在x轴上方时,
三种情况分析即可;②先求出直线BC的解析式,当点P在x轴上方时,![]() ,可得出直线BP的解析式为:
,可得出直线BP的解析式为:![]() ,求出与抛物线的交点即可;当点P在x轴下方时,可得出直线BP的解析式为:
,求出与抛物线的交点即可;当点P在x轴下方时,可得出直线BP的解析式为:![]() ,求出与抛物线的交点即可.
,求出与抛物线的交点即可.
解:(1)把![]() 代入
代入![]() 得:
得:![]()
则B的坐标为![]() ,
,
把![]() 代入
代入![]() 中
中
得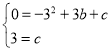
解得:![]()
∴抛物线的解析式的为:![]() .
.
(2) ∵![]()
∴![]()
又![]() 轴
轴
∴![]()
∴![]()
① 当![]() 时,如图1,
时,如图1,
∵△PBD是等腰直角三角形,
∴![]()
解得:![]() ;
;
当![]() 时,如图2,
时,如图2,
过点B作BG⊥PD,△PBD是等腰直角三角形,
∴![]() .
.
∴![]() ,
,
解得:![]() ;
;
当![]() 时,如图3,
时,如图3,
过点B作BF⊥PD,△BFD是等腰直角三角形,
∴![]() .
.
∴![]() ,
,
解得:![]() ;
;

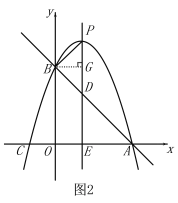
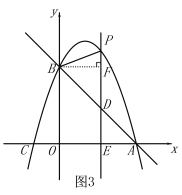
综上所述,点E的坐标为![]() ,
,![]() 或
或![]() .
.
② 根据抛物线解析式可得出点![]()
∴直线CB的解析式为:![]()
当点P在x轴上方时,如图1,
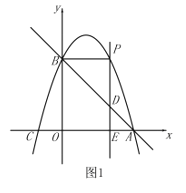
∵![]() ,
,![]()
∴![]()
∴直线BP的解析式为:![]()
∴![]()
解得:![]() (舍去)
(舍去)
当点P在x轴下方时,如下图所示:
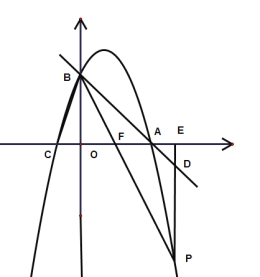
∵![]() ,
,![]()
∴![]()
∴![]()
∴直线BP的解析式为:![]()
∴![]()
解得:![]() (舍去)
(舍去)
∴m的值为![]() 或5.
或5.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】对于某一函数给出如下定义:对于任意实数m, 当自变量x≥m时,函数y关于x的函数图象为![]() ,将G沿直线x=m翻折后得到的函数图象为
,将G沿直线x=m翻折后得到的函数图象为![]() ,函数G的图象由
,函数G的图象由![]() 和
和![]() 两部分共同组成,则函数G为原函数的“对折函数”,如函数y=x(x≥2)的对折函数为
两部分共同组成,则函数G为原函数的“对折函数”,如函数y=x(x≥2)的对折函数为![]()
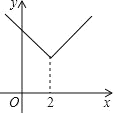
(1)写出函数y =2x+1(x≥ 1)的对折函数;
(2)若函数y =2x2(x≥![]() )的对折函数与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,求△ABC的周长;
)的对折函数与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,求△ABC的周长;
(3)若点P(m,5)在函数y =![]() 4( x≥1)的对折函数的图象上,求m的值;
4( x≥1)的对折函数的图象上,求m的值;
(4)当函数y=![]() 4(x≥n)的对折函数与x轴有不同的交点个数时,直接写出n的取值范围
4(x≥n)的对折函数与x轴有不同的交点个数时,直接写出n的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是指一个国家(或地区)在一定时期内生产活动的最终成果,常被公认为是衡量经济状况的最佳指标.截止2020年4月27日,对除西藏外的30个省区市第一季度有关
是指一个国家(或地区)在一定时期内生产活动的最终成果,常被公认为是衡量经济状况的最佳指标.截止2020年4月27日,对除西藏外的30个省区市第一季度有关![]() 的数据进行收集、整理、描述和分析.下面给出了部分信息:
的数据进行收集、整理、描述和分析.下面给出了部分信息:
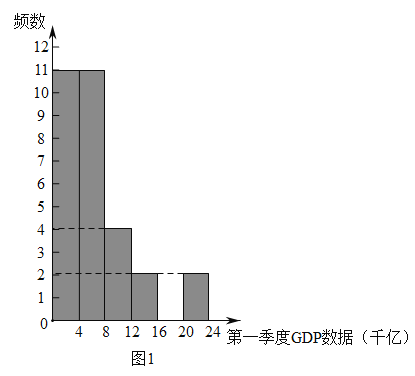
a.各省区市![]() 数据的频数分布直方图,如图1(数据分成6组,各组是
数据的频数分布直方图,如图1(数据分成6组,各组是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ):
):
b.2020年第一季度![]() 数据在这一组的是:4.6 4.9 5.0 5.1 5.3 5.4 6.3 7.4 7.5 7.8 7.8
数据在这一组的是:4.6 4.9 5.0 5.1 5.3 5.4 6.3 7.4 7.5 7.8 7.8
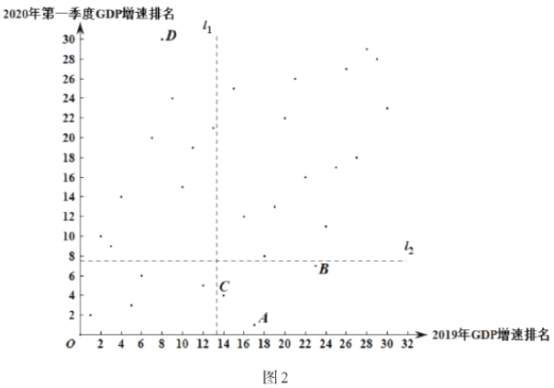
c.30个省区市2020年第一季度及2019年![]() 增速排名统计图,如图2:
增速排名统计图,如图2:
d.北京2020年第一季度![]() 数据约为7.5千亿,
数据约为7.5千亿,![]() 增速排名为第22.
增速排名为第22.
根据以上信息,回答下列问题:
(1)在30个省区市中,北京2020年第一季度![]() 的数据排名第______.
的数据排名第______.
(2)在30个省区市2020年第一季度及2019年![]() 增速排名统计图中,请在图中用“○”圈出代表北京的点.
增速排名统计图中,请在图中用“○”圈出代表北京的点.
(3)2020年第一季度![]() 增速排名位于北京之后的几个省份中,2019年
增速排名位于北京之后的几个省份中,2019年![]() 增速排名的最好成绩是第_______.
增速排名的最好成绩是第_______.
(4)下列推断合理的是___________.
①与2019年![]() 增速排名相比,在疫情冲击下,2020年全国第一季度增速排名,部分省市有较大下滑,如D代表的湖北排名下滑最多.
增速排名相比,在疫情冲击下,2020年全国第一季度增速排名,部分省市有较大下滑,如D代表的湖北排名下滑最多.
②A、B、C分别代表的新疆、广西、青海位于西部地区,多为人口净流出或少量净流入,经济发展主要依靠本地劳动力供给,疫后复工复产效率相对较高,相对于2019年![]() 增速排名位置靠前.
增速排名位置靠前.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.深圳市环境卫生局为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:
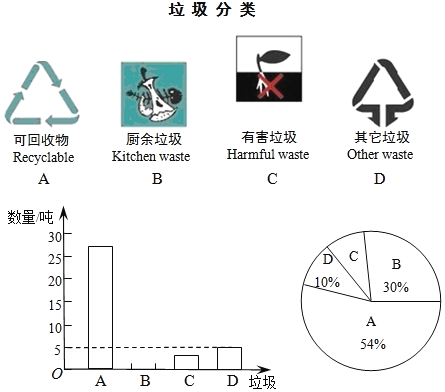
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图中,产生的有害垃圾C所对应的圆心角为 度;
(3)调查发现,在可回收物中塑料类垃圾占13%,每回收1吨塑料类垃圾可获得0.5吨二级原料.假设深圳市每天产生的生活垃圾为28500吨,且全部分类处理,那么每天回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,分别与AC,BC交于点E,F. 过点F作⊙O的切线交AB于点M.
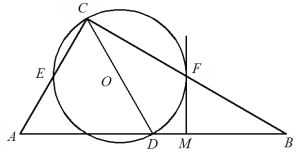
(1)求证:MF⊥AB;
(2)若⊙O的直径是6,填空:
①连接OF,OM,当FM= 时,四边形OMBF是平行四边形;
②连接DE,DF,当AC= 时,四边形CEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级有学生400人,为了解这个年级普及安全教育的情况,随机抽取了20名学生,进行安全教育考试,测试成绩(百分制)如下:
71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
(1)请补全七年级20名学生安全教育测试成绩频数分布直方图;
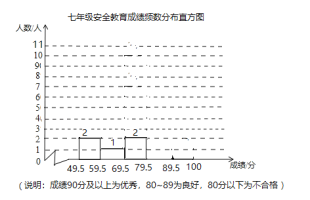
(2)样本数据的平均数、中位数、众数、优秀率如下表所示,请补充完整;
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 85.4 |
|
|
|
(3)估计七年级成绩优秀的学生人数约为_________人.
(4)学校有安全教育老师男女各2名,现从这4名老师中随机挑选2名参加“安全教育”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与坐标轴交于
与坐标轴交于![]() 两点,与双曲线
两点,与双曲线![]() 交于点
交于点![]() , 过点
, 过点![]() 作
作![]() 轴,且
轴,且![]() ,则以下结论错误的是( )
,则以下结论错误的是( )
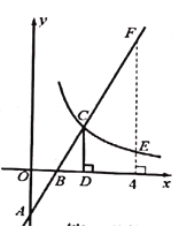
A.![]()
B.当![]() 时,
时,![]()
C.当![]() 时,
时,![]()
D.当![]() 时,
时,![]() 随
随![]() 的增大而增大,
的增大而增大,![]() 随
随![]() 的增大而减小
的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,存在半径为2,圆心为(0,2)的
中,存在半径为2,圆心为(0,2)的![]() ,点
,点![]() 为
为![]() 上的任意一点,线段
上的任意一点,线段![]() 绕点
绕点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,如果点
,如果点![]() 在线段
在线段![]() 上,那么称点
上,那么称点![]() 为
为![]() 的“限距点”.
的“限距点”.
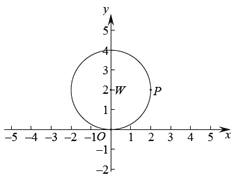
(1)在点![]() 中,
中,![]() 的“限距点”为____________________________;
的“限距点”为____________________________;
(2)如果过点![]() 且平行于
且平行于![]() 轴的直线
轴的直线![]() 上始终存在
上始终存在![]() 的“限距点”,画出示意图并直接写出
的“限距点”,画出示意图并直接写出![]() 的取值范围;
的取值范围;
(3)![]() 的圆心为
的圆心为![]() ,半径为1,如果
,半径为1,如果![]() 上始终存在
上始终存在![]() 的“限距点”,请直接写出
的“限距点”,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学进校时需要从学校大门A、B、C三个入口处中的任意一处测量体温,体温正常方可进校.
(1)甲同学在A入口处测量体温的概率是 ;
(2)求甲、乙两位同学在同一入口处测量体温的概率.(用“画树状图”或“列表”的方法写出分析过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com