【题目】某公司生产的一种产品按照质量由高到低分为A，B，C，D四级，为了增加产量、提高质量，该公司改进了一次生产工艺，使得生产总量增加了一倍．为了解新生产工艺的效果，对改进生产工艺前、后的四级产品的占比情况进行了统计，绘制了如下扇形图：
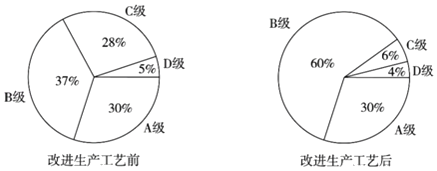
根据以上信息，下列推断合理的是（ ）
A.改进生产工艺后，A级产品的数量没有变化
B.改进生产工艺后，B级产品的数量增加了不到一倍
C.改进生产工艺后，C级产品的数量减少
D.改进生产工艺后，D级产品的数量减少
【答案】C
【解析】
设原生产总量为1，则改进后生产总量为2，所以原A、B、C、D等级的生产量为0.3、0.37、0.28、0.05，改进后四个等级的生产量为0.6、1.2、0.12、0.08，据此逐一判断即可得．
设原生产总量为1，则改进后生产总量为2，
所以原A、B、C、D等级的生产量为0.3、0.37、0.28、0.05，
改进后四个等级的生产量为0.6、1.2、0.12、0.08，
A．改进生产工艺后，A级产品的数量增加，此选项错误；
B．改进生产工艺后，B级产品的数量增加超过三倍，此选项错误；
C．改进生产工艺后，C级产品的数量减少，此选项正确；
D．改进生产工艺后，D级产品的数量增加，此选项错误；
故选：C．
阅读快车系列答案科目：初中数学 来源： 题型：
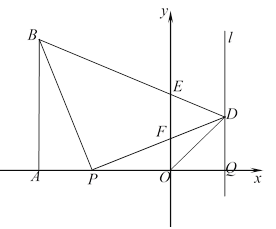
【题目】如图，在平面直角坐标系
中，
轴于点
．点
从点出发，以每秒
个单位长度的速度沿
轴向点
运动；点
从点同时出发，以相同的速度沿轴的正方向运动，运动时间
．过点作平行于
轴的直线
，连接
，过点作
交直线于点
，
、
与轴分别交于点
、
，连接
．
（1）当
时，试求
的值；
（2）当为
中点时，试求
的值；
（3）是否存在这样的
，使得
与
的面积相等？若存在，求出所有符合条件的；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
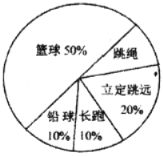
【题目】九年级（1）班学生在完成课题学习“体质健康测试中的数据分析”后，利用课外活动时间积极参加体育锻炼，每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练，训练后都进行了测试．现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图．请你根据上面提供的信息回答下列问题：
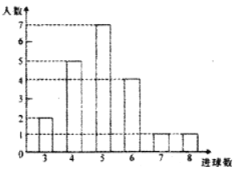
（1）该班共有学生______人，训练后篮球定时定点投篮平均每个人的进球数是_______．
（2）老师决定从选择铅球训练的
名男生和
名女生中任选两名学生先进行测试，请用列表或画树形图的方法求恰好选中两名男生的概率．
项目选择人数情况统计图
训练后篮球定时定点投篮测试进球数统计图
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场计划购进
、
两种新型节能台灯共
盏，这两种台灯的进价、售价如表所示：
（
）若商场预计进货款为
元，则这两种台灯各购进多少盏？
（
）若商场规定
型台灯的进货数量不超过
型台灯数量的
倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
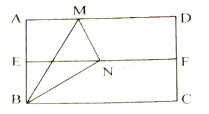
【题目】如图，在矩形纸片
中，
，对折矩形纸片，使
与
重合，折痕为
，展平后再过点
折叠，使点
落在上的点
，折痕为
．再次展平，连接
，
，有下列结论：①
；②
与
相似；③的长为
：④若
分别为线段
上的动点（不包含端点），则
的最小值是
．其中正确结论的序号是__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
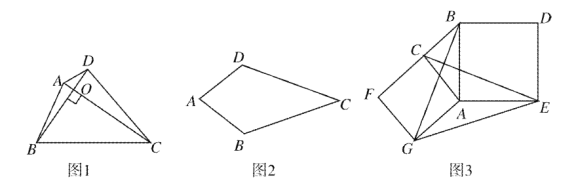
【题目】如图1，对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解：如图2，在四边形
中，
，问四边形是垂美四边形吗?请说明理由；
(2)性质探究：如图1，四边形的对角线
交于点
，
.
试证明：
；
(3)解决问题：如图3，分别以
的直角边
和斜边
为边向外作正方形
和正方形
，连结
.已知
，求
的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着生活节奏的加快以及智能手机的普及，外卖点餐逐渐成为越来越多用户的餐饮消费习惯．由此催生了一批外卖点餐平台，已知某外卖平台的送餐费用与送餐距离有关（该平台只给5千米范围内配送），为调査送餐员的送餐收入，现从该平台随机抽取80名点外卖的用户进行统计，按送餐距离分类统计结果如下表：
送餐距离x（千米） | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
（1）从这80名点外卖的用户中任取一名用户，该用户的送餐距离不超过3千米的概率为 ；
（2）以这80名用户送餐距离为样本，同一组数据取该小组数据的中间值（例如第二小组（1＜x ≤2）的中间值是1.5），试估计利用该平台点外卖用户的平均送餐距离；
（3）若该外卖平台给送餐员的送餐费用与送餐距离有关，不超过2千米时，每份3元；超过2千米但不超4千米时，每份5元；超过4千米时，每份9元． 以给这80名用户所需送餐费用的平均数为依据，若送餐员一天的目标收入不低于150元，试估计一天至少要送多少份外卖？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情境：
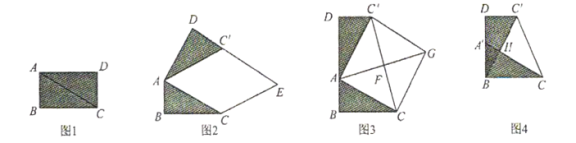
在综合与实践课上，老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1，将矩形纸片
沿对角线
剪开，得到
和
.并且量得
，
.
操作发现：
（1）将图1中的以点
为旋转中心，按逆时针方向旋转
，使
，得到如图2所示的
，过点
作
的平行线，与
的延长线交于点
，则四边形
的形状是________.
（2）创新小组将图1中的以点为旋转中心，按逆时针方向旋转，使
、、
三点在同一条直线上，得到如图3所示的，连接
，取的中点
，连接
并延长至点
，使
，连接
、
，得到四边形
，发现它是正方形，请你证明这个结论.
实践探究：
（3）缜密小组在创新小组发现结论的基础上，进行如下操作：将沿着
方向平移，使点与点重合，此时点平移至
点，
与
相交于点
，如图4所示，连接，试求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)问题发现
如图
， 在
和
中，
，
，
， 连接
，
交于点
．填空：①
的值为 ：②
的度数为
(2)类比探究
如图
， 在和中，
，
， 连接交的延长线于点．请求出能的值及的度数， 并说明理由；
(3)拓展延伸
在
的条件下， 将绕点
在平面内旋转，
所在直线交于点， 若
，
，请直接写出当点
与点重合时的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
