
科目:初中数学 来源: 题型:
 如图是9×7的正方形点阵,其水平方向和竖直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:
如图是9×7的正方形点阵,其水平方向和竖直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012年人教版初中数学九年级上25.2列举法求概率练习卷(解析版) 题型:解答题
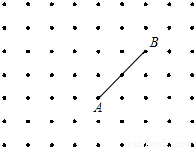
如图是9×7的正方形点阵,其水平方向和竖起直方向的两格点间的长度都为1个单位,以这些点为顶点的三角形称为格点三角形.请通过画图分析、探究回答下列问题:

(1)请在图中画出以AB为边且面积为2的一个网格三角形;
(2)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形的面积为2的概率;
(3)任取该网格中能与A、B构成三角形的一点M,求以A、B、M为顶点的三角形为直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (9-1)=4,
(9-1)=4, (9+1)=5和
(9+1)=5和 (25-1)=12,
(25-1)=12, (25+1)=13
(25+1)=13 (n2-1),弦=
(n2-1),弦= (n2+1)分别写出能表示7,24,25的股和弦的算式?
(n2+1)分别写出能表示7,24,25的股和弦的算式?查看答案和解析>>
科目:初中数学 来源:《25.2 列举法求概率》2010年同步练习1(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com