练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图所示，有一块边长为24m的正方形绿地，绿地周边是小路，在绿地旁边的B处有健身器材，BC=7m．请你算一算，如果居住在A处的居民为了走近路而不惜践踏草地直接从A到B，这样比沿着绿地周边的小路，仅少走多少米？
    考点：勾股定理的应用
    专题：
    分析：根据题意可以知道AC和BC的长度，从而构造直角三角形，根据勾股定理就可求出斜边AB的距离，进一步即可求解．
    解答：解：由题意可知AB=
    		AC2+BC2
    =
    		242+72
    =25m，
    故居民直接到B时要走AB=25m，若A居民不践踏绿地应走AC+BC=24+7=31m
    AC+BC-AB=31-25=6m
    故仅少走6米．
    点评：本题考查正确运用勾股定理．善于观察题目的信息是解题以及学好数学的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    一筐苹果4千克，增加
    1
    2
    后，列出的算式为（　　）
    A、4+
    1
    2
    B、4×（1+
    1
    2
    ）
    C、4÷（1+）
    D、4×（1-
    1
    2
    ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    阅读下面的解题过程：
    计算：（
    2
    3
    ）2-（-2）×（
    1
    4
    -
    1
    2
    ）+
    1
    6
    ．
    解：原式=
    4
    3
    -（-2）×（
    1
    4
    -
    1
    2
    ）+
    1
    6
    …（第一步）
    =
    4
    3
    -（
    1
    2
    -1）+
    1
    6
    …（第二步）
    =
    4
    3
    +
    1
    2
    +
    1
    6
    …（第三步）
    =2…（第四步）
    回答下列问题：
    （1）上面解题过程中有两处错误，第一处：是第
     
    步，错误的原因是
     
    ；第二处：是第
     
    步，错误的原因是
     
    ．
    （2）直接写出正确的结果是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算题：
    （1）2
    		12
    +3
    		48
    ；
    （2）
    		8
    -
    		18
    		2
    ；
    （3）（
    		13
    +3（（
    		13
    -3）；
    （4）（
    9
    2
    -
    		98
    3
    ）×2
    		2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    先化简，再求值：
    [（x-2y）2+（x-2y）（x+2y）-2x（2x-y）]÷2x，其中x=-1，y=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

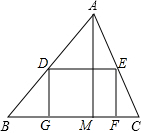    如图，△ABC是一块锐角三角形余料，AM⊥BC，BC=10，AM=6，要把它加工成两邻边：
    DE
    DG
    =
    5
    3
    矩形零件，使矩形的一边GF在BC上，其余两个顶点分别在AB、AC上．求矩形DEFG的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，在△ABC中，∠ABC和∠ACB的平分线交于点D．过点D作EF∥BC交AB于点E，交AC于点F，若BE+CF=9cm，求线段EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

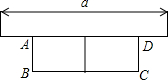    如图，有长为24米的篱笆，一面利用墙（强的最大可用长度为a为12米），围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，花圃ABCD的面积为S米2．
    （1）当x为何值时，花圃ABCD的面积最大？最大面积是多少？
    （2）如果要围成面积为45米2的花圃，AB的长是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

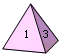    如图，均匀的正四面体的各面依次标有1，2，3，4四个数字．小明做了60次投掷试验，结果统计如下：
    朝下数字1234
    出现的次数16201410
    （1）计算上述试验中“4朝下”的频率是
     
    ；
    （2）随机投掷正四面体两次，请用列表或画树状图法，求两次朝下的数字之和大于4的概率．

    查看答案和解析>>

    同步练习册答案