
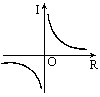
如图,在公式I=![]() 中,当电压U一定时,电流I与电阻R之间的函数关系可用图像表示为
中,当电压U一定时,电流I与电阻R之间的函数关系可用图像表示为
[ ]

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源:吉林省长春外国语学校2011-2012学年八年级第一次月考数学试题 题型:044
我们已经知道了一些特殊的勾股数,如三个连续整数中的勾股数:3、4、5;三个连续的偶数中的勾股数6、8、10;由此发现勾股数的正整数倍仍然是勾股数.
(1)如果a、b、c是一组勾股数,即满足a2+b2=c2,求证:ka、kb、kc(k为正整数)也是一组勾股数.
(2)另外利用一些构成勾股数的公式也可以写出许多勾股数,如
①公式a=m2-n2,b=2mn,c=m2+n2(m、n为整数,m>n,m>1)
②世界上第一次给出的勾股数的公式,被收集在《九章算术》中a=![]() (m2-n2),b=mn,c=
(m2-n2),b=mn,c=![]() (m2+n2)(m、n为正整数,m>n)
(m2+n2)(m、n为正整数,m>n)
③公元前427-公元前347,由柏拉图提出的公式a=n2-1,b=2n,c=n2+1(n>1,且n为整数)
④毕达哥拉斯学派提出的公式a=2n+1,b=2n2+2n,c=2n2+2n+1(n为正整数)
请你在上述的四个公式中选择一种加以证明,满足公式的a、b、c是一组勾股数
(3)请根据你在(2)中所选的公式写出一组勾股数.
查看答案和解析>>
科目:初中数学 来源:2013年吉林省长春市高级中等学校招生考试数学 题型:044
如图,在平面直角坐标系中,抛物线y=ax2+bx-2与x轴交于点A(-1,0)、B(4,0).点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.

(1)求这条抛物线所对应的函数关系式.
(2)求点C在这条抛物线上时m的值.
(3)将线段CN绕点N逆时针旋转90°后,得到对应线段DN.
①当点D在这条抛物线的对称轴上时,求点D的坐标.
②以DN为直角边作等腰直角三角形DNE,当点E在这条抛物线的对称轴上时,直接写出所有符合条件的m值.
[参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为![]() ]
]
查看答案和解析>>
科目:初中数学 来源:2013届江苏省南京市鼓楼区中考二模数学试卷(带解析) 题型:解答题
【提出问题】
如图①,在梯形ABCD中,AD//BC,AC、BD交于点E,∠BEC=n°,若AD=a,BC=b,则梯形ABCD的面积最大是多少?
【探究过程】
小明提出:可以从特殊情况开始探究,如图②,在梯形ABCD中,AD//BC,AC⊥BD,若AD=3,BC=7,则梯形ABCD的面积最大是多少?
如图③,过点D做DE//AC交BC的延长线于点E,那么梯形ABCD的面积就等于△DBE的面积,求梯形ABCD的面积最大值就是求△DBE的面积最大值.如果设AC=x,BD=y,那么S△DBE=xy.
以下是几位同学的对话:
A同学:因为y= ,所以S△DBE=x
,所以S△DBE=x ,求这个函数的最大值即可.
,求这个函数的最大值即可.
B同学:我们知道x2+y2=100,借助完全平方公式可求S△DBE=xy的最大值
C同学:△DBE是直角三角形,底BE=10,只要高最大,S△DBE就最大,我们先将所有满足BE=10的直角△DBE都找出来,然后在其中寻找高最大的△DBE即可.


(1)请选择A同学或者B同学的方法,完成解题过程.
(2)请帮C同学在图③中画出所有满足条件的点D,并标出使△DBE面积最大的点D1.(保留作图痕迹,可适当说明画图过程)
【解决问题】
根据对特殊情况的探究经验,请在图①中画出面积最大的梯形ABCD的顶点D1,并直接写出梯形ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省南京市鼓楼区中考二模数学试卷(解析版) 题型:解答题
【提出问题】
如图①,在梯形ABCD中,AD//BC,AC、BD交于点E,∠BEC=n°,若AD=a,BC=b,则梯形ABCD的面积最大是多少?
【探究过程】
小明提出:可以从特殊情况开始探究,如图②,在梯形ABCD中,AD//BC,AC⊥BD,若AD=3,BC=7,则梯形ABCD的面积最大是多少?
如图③,过点D做DE//AC交BC的延长线于点E,那么梯形ABCD的面积就等于△DBE的面积,求梯形ABCD的面积最大值就是求△DBE的面积最大值.如果设AC=x,BD=y,那么S△DBE=xy.
以下是几位同学的对话:
A同学:因为y= ,所以S△DBE=x
,所以S△DBE=x ,求这个函数的最大值即可.
,求这个函数的最大值即可.
B同学:我们知道x2+y2=100,借助完全平方公式可求S△DBE=xy的最大值
C同学:△DBE是直角三角形,底BE=10,只要高最大,S△DBE就最大,我们先将所有满足BE=10的直角△DBE都找出来,然后在其中寻找高最大的△DBE即可.

(1)请选择A同学或者B同学的方法,完成解题过程.
(2)请帮C同学在图③中画出所有满足条件的点D,并标出使△DBE面积最大的点D1.(保留作图痕迹,可适当说明画图过程)
【解决问题】
根据对特殊情况的探究经验,请在图①中画出面积最大的梯形ABCD的顶点D1,并直接写出梯形ABCD面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com