
| A. | $\root{3}{0.177}$≈0.5615 | B. | $\root{3}{0.0177}$≈0.5615 | C. | $\root{3}{1.77}$≈0.5165 | D. | $\root{3}{17.7}$≈56.15 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2•a3=a6 | B. | (-2xy2)3=-8x3y5 | C. | 2a-3=$\frac{1}{2{a}^{3}}$ | D. | (-a)3÷(2a)2=-$\frac{1}{4}$a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{7}{25}$ | D. | $\frac{56}{65}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
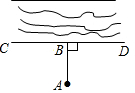 某工程队计划把河水引到水池A中,他们先过A点作AB⊥CD,垂足为B,然后沿AB开渠,可以节约人力、物力和财力,这样设计的数学依据是( )
某工程队计划把河水引到水池A中,他们先过A点作AB⊥CD,垂足为B,然后沿AB开渠,可以节约人力、物力和财力,这样设计的数学依据是( )| A. | 两点之间线段最短 | B. | 经过两点有且只有一条直线 | ||
| C. | 垂直定义 | D. | 垂线段最短 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com