
ЁОЬтФПЁПШчЭМ1ЃЌЕу![]() дке§ЗНаЮ
дке§ЗНаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЩЯЃЌе§ЗНаЮ
ЩЯЃЌе§ЗНаЮ![]() ЕФБпГЄЪЧ
ЕФБпГЄЪЧ![]() ЃЌ
ЃЌ![]() ЕФСНЬѕжБНЧБп
ЕФСНЬѕжБНЧБп![]() ЗжБ№НЛБп
ЗжБ№НЛБп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉВйзїЗЂЯжЃКШчЭМ2ЃЌЙЬЖЈЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ШЦЕу
ШЦЕу![]() а§зЊЃЌЕБ
а§зЊЃЌЕБ![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮЃЎ
ЪЧе§ЗНаЮЃЎ
ЬюПеЃКЂйЕБ![]() ЪБЃЌЫФБпаЮ
ЪБЃЌЫФБпаЮ![]() ЕФБпГЄЪЧ_____ЃЛ
ЕФБпГЄЪЧ_____ЃЛ
ЂкЕБ![]() ЃЈ
ЃЈ![]() ЪЧе§ЪЕЪ§ЃЉЪБЃЌЫФБпаЮ
ЪЧе§ЪЕЪ§ЃЉЪБЃЌЫФБпаЮ![]() ЕФУцЛ§ЪЧ______ЃЛ
ЕФУцЛ§ЪЧ______ЃЛ
ЃЈ2ЃЉВТЯыТлжЄЃКШчЭМ3ЃЌНЋЫФБпаЮ![]() ЕФаЮзДИФБфЮЊОиаЮЃЌ
ЕФаЮзДИФБфЮЊОиаЮЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() дкОиаЮ
дкОиаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЃЌ
ЃЌ![]() ЕФСНЬѕжБНЧБп
ЕФСНЬѕжБНЧБп![]() ЗжБ№НЛБп
ЗжБ№НЛБп![]() гкЕу
гкЕу![]() ЃЌЙЬЖЈЕу
ЃЌЙЬЖЈЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ШЦЕу
ШЦЕу![]() а§зЊЃЌдђ
а§зЊЃЌдђ![]() ______ЃЛ
______ЃЛ
ЃЈ3ЃЉЭиеЙЬНОПЃКШчЭМ4ЃЌЕБЫФБпаЮ![]() ТњзуЬѕМўЃК
ТњзуЬѕМўЃК![]() ЃЌ
ЃЌ![]() ЃЌЪБЃЌЕу
ЃЌЪБЃЌЕу![]() дкЖдНЧЯп
дкЖдНЧЯп![]() ЩЯЃЌ
ЩЯЃЌ![]() ЗжБ№НЛБп
ЗжБ№НЛБп![]() гкЕу
гкЕу![]() ЃЌЙЬЖЈЕу
ЃЌЙЬЖЈЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ШЦЕу
ШЦЕу![]() а§зЊЃЌЧыЬНОП
а§зЊЃЌЧыЬНОП![]() ЕФжЕЃЌВЂЫЕУїРэгЩЃЎ
ЕФжЕЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЌРэгЩМћНтЮі
ЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
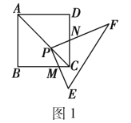
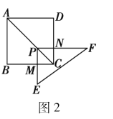
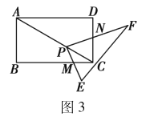
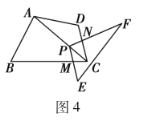
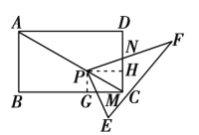
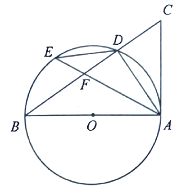
ЃЈ1ЃЉЂйЯШХаЖЈЁїPMCЁзЁїABCЃЌдйИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§НјааЧѓНтЃЛЂкЯШгУЂйжаЕФЗНЗЈЧѓЕУе§ЗНаЮPMCNЕФБпГЄЃЛ
ЃЈ2ЃЉЯШЙ§PзїPGЁЭBCгкGЃЌзїPHЁЭCDгкHЃЌХаЖЈЁїPGMЁзЁїPHNЃЌдйИљОнЯрЫЦШ§НЧаЮЕФаджЪвдМАЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэНјааЭЦЕММЦЫуМДПЩЃЛ
ЃЈ3ЃЉЯШЙ§PзїPGЁЮABЃЌзїPHЁЮADЃЌВЂНсКЯЬѕМўЁЯB+ЁЯD=180ЁуЃЌХаЖЈЁїPGMЁзЁїPHNЃЌдйИљОнЯрЫЦШ§НЧаЮЕФаджЪвдМАЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэНјааЭЦЕММЦЫуМДПЩЃЎ
ЃЈ1ЃЉЂй![]()
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁпЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌЁрЫФБпаЮ
ЪЧе§ЗНаЮЃЌЁрЫФБпаЮ![]() ЕФБпГЄЪЧ
ЕФБпГЄЪЧ![]() ЃЎ
ЃЎ
Ђк![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁрЫФБпаЮ
ЃЌЁрЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉ![]()
ШчЭМЃЌ
Й§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ЃЌгж
ЃЌгж![]() ЃЌ
ЃЌ![]()
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎгЩ
ЃЎгЩ![]() ЃЌ
ЃЌ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉ![]() ЃЎРэгЩШчЯТЃК
ЃЎРэгЩШчЯТЃК

ШчЭМЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гж![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
гЩ![]() ЃЌ
ЃЌ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ


 вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ
вЛЯпУћЪІШЈЭўзївЕБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇЩњВњЛЏЗЪЕФзмШЮЮёвЛЖЈЃЌЦНОљУПЬьЛЏЗЪВњСПyЃЈЖжЃЉгыЭъГЩЩњВњШЮЮёЫљашвЊЕФЪБМфxЃЈЬьЃЉжЎМфГЩЗДБШР§ЙиЯЕЃЌШчЙћУПЬьЩњВњЛЏЗЪ125ЖжЃЌФЧУДЭъГЩзмШЮЮёашвЊ7ЬьЃЎ
ЃЈ1ЃЉЧѓyЙигкxЕФКЏЪ§БэДяЪНЃЌВЂжИГіБШР§ЯЕЪ§ЃЛ
ЃЈ2ЃЉШєвЊ5ЬьЭъГЩзмШЮЮёЃЌдђУПЬьВњСПгІДяЕНЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
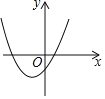
ЁОЬтФПЁПвбжЊЃКШчЭМЪЧyЃНax2+2xЉ1ЕФЭМЯѓЃЌФЧУДax2+2xЉ1ЃН0ЕФИљПЩФмЪЧЯТСаФФЗљЭМжаХзЮяЯпгыжБЯпЕФНЛЕуКсзјБъЃЈЁЁЁЁЃЉ
A.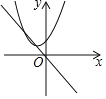 B.
B.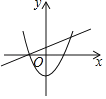
C.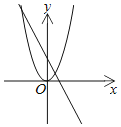 D.
D.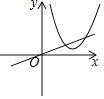
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯТСаУќЬтЃКЂйЖдНЧЯпЛЅЯрДЙжБЕФЫФБпаЮЪЧСтаЮЃЛЂкШє![]() ЃЌдђ
ЃЌдђ![]() ЃЛЂлСНИіЮЛЫЦЭМаЮвЛЖЈЪЧЯрЫЦЭМаЮЃЛЂмШє
ЃЛЂлСНИіЮЛЫЦЭМаЮвЛЖЈЪЧЯрЫЦЭМаЮЃЛЂмШє![]() ЃЌдђ
ЃЌдђ![]() ЃЛЦфжадУќЬтЪЧецУќЬтФцУќЬтЪЧМйУќЬтЕФгаЃЈ ЃЉ
ЃЛЦфжадУќЬтЪЧецУќЬтФцУќЬтЪЧМйУќЬтЕФгаЃЈ ЃЉ
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЃН4ЃЌЩфЯпBMКЭABЛЅЯрДЙжБЃЌЕуDЪЧABЩЯЕФвЛИіЖЏЕуЃЌЕуEдкЩфЯпBMЩЯЃЌBEЃН![]() DBЃЌзїEFЁЭDEВЂНиШЁEFЃНDEЃЌСЌНгAFВЂбгГЄНЛЩфЯпBMгкЕуC.ЩшBEЃНxЃЌBCЃНyЃЌдђyЙигкxЕФКЏЪ§НтЮіЪНЮЊ(ЁЁЁЁ)
DBЃЌзїEFЁЭDEВЂНиШЁEFЃНDEЃЌСЌНгAFВЂбгГЄНЛЩфЯпBMгкЕуC.ЩшBEЃНxЃЌBCЃНyЃЌдђyЙигкxЕФКЏЪ§НтЮіЪНЮЊ(ЁЁЁЁ)
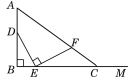
A.Ѓ![]() B.Ѓ
B.Ѓ![]() C.Ѓ
C.Ѓ![]() D.Ѓ
D.Ѓ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ4ЃЌЕуEЃЌFЗжБ№дкБпABЃЌADЩЯЃЌЧвЁЯECFЃН45ЁуЃЌCFЕФбгГЄЯпНЛBAЕФбгГЄЯпгкЕуGЃЌCEЕФбгГЄЯпНЛDAЕФбгГЄЯпгкЕуHЃЌСЌНгACЃЌEFЃЎЃЌGHЃЎ
ЃЈ1ЃЉЬюПеЃКЁЯAHCЁЁ ЁЁЁЯACGЃЛЃЈЬюЁАЃОЁБЛђЁАЃМЁБЛђЁАЃНЁБЃЉ
ЃЈ2ЃЉЯпЖЮACЃЌAGЃЌAHЪВУДЙиЯЕЃПЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЩшAEЃНmЃЌ
ЂйЁїAGHЕФУцЛ§SгаБфЛЏТ№ЃПШчЙћБфЛЏЃЎЧыЧѓГіSгыmЕФКЏЪ§ЙиЯЕЪНЃЛШчЙћВЛБфЛЏЃЌЧыЧѓГіЖЈжЕЃЎ
ЂкЧыжБНгаДГіЪЙЁїCGHЪЧЕШбќШ§НЧаЮЕФmжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮ![]() жаЃЌЯпЖЮ
жаЃЌЯпЖЮ![]() ШЦОиаЮЭтвЛЕу
ШЦОиаЮЭтвЛЕу![]() ЫГЪБеыа§зЊЃЌа§зЊНЧЮЊ
ЫГЪБеыа§зЊЃЌа§зЊНЧЮЊ![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕуЕФЖдгІЕу
ЕуЕФЖдгІЕу![]() ТфдкЩфЯп
ТфдкЩфЯп![]() ЩЯЃЌ
ЩЯЃЌ![]() ЕуЕФЖдгІЕу
ЕуЕФЖдгІЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯЃЎ
ЕФбгГЄЯпЩЯЃЎ
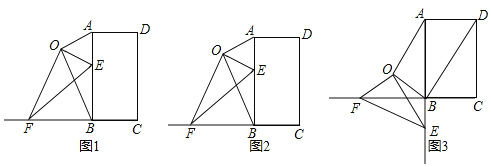
ЃЈ1ЃЉШчЭМ1ЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌдђ
ЃЌдђ![]() гы
гы![]() ЕФДѓаЁЙиЯЕЮЊ______________ЃЎ
ЕФДѓаЁЙиЯЕЮЊ______________ЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕу![]() ЮЛгкЯпЖЮ
ЮЛгкЯпЖЮ![]() ЩЯЪБЃЌЧѓжЄЃК
ЩЯЪБЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБЕу![]() ЮЛгкЯпЖЮ
ЮЛгкЯпЖЮ![]() ЕФбгГЄЯпЩЯЪБЃЌ
ЕФбгГЄЯпЩЯЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓЫФБпаЮ
ЃЌЧѓЫФБпаЮ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌвд
жаЃЌвд![]() ЮЊжБОЖзїЁб
ЮЊжБОЖзїЁб![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЮЊЛЁ
ЮЊЛЁ![]() ЩЯвЛЕуЃЌСЌНг
ЩЯвЛЕуЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() .
.
(1)Шє![]() ЃЌЧѓжЄ:
ЃЌЧѓжЄ:![]() ЮЊЁб
ЮЊЁб![]() ЕФЧаЯп;
ЕФЧаЯп;
(2)Шє![]() ЃЌЧѓжЄ:
ЃЌЧѓжЄ:![]() ЦНЗж
ЦНЗж![]() ;
;
(3)дк(2)ЕФЬѕМўЯТЃЌШє![]() ЃЌЧѓЁб
ЃЌЧѓЁб![]() ЕФАыОЖ.
ЕФАыОЖ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫБЃЛЄЩњЬЌЛЗОГЃЌФГЙЄГЇдквЛЖЮЪБМфФкЯоВњВЂЭЖШызЪН№НјаажЮЮлИФдьЃЎШчЭМУшЪіЕФЪЧдТРћШѓy(ЭђдЊ)КЭдТЗнxжЎМфЕФБфЛЏЙиЯЕЃЌжЮЮлИФдьЭъГЩЧАЪЧЗДБШР§КЏЪ§ЭМЯѓЕФвЛВПЗжЃЌжЮЮлИФдьЭъГЩКѓЪЧвЛДЮКЏЪ§ЭМЯѓЕФвЛВПЗжЃЌдђЯТСаЫЕЗЈВЛе§ШЗЕФЪЧ(ЁЁЁЁ)

A.5дТЗнИУГЇЕФдТРћШѓзюЕЭ
B.жЮЮлИФдьЭъГЩКѓЃЌУПдТРћШѓБШЧАвЛИідТдіМг30ЭђдЊ
C.жЮЮлИФдьЧАКѓЃЌЙВга6ИідТЕФдТРћШѓВЛГЌЙ§120ЭђдЊ
D.жЮЮлИФдьЭъГЩКѓЕФЕк8ИідТЃЌИУГЇдТРћШѓДяЕН300ЭђдЊ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com