
【题目】如图,A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=EF,AC=BD.求证:△ACF≌△BDE.

科目:初中数学 来源: 题型:
【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交与点P,若∠CAP=50°,则∠BPC的度是( )

A. 80° B. 60° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南海海域面积约为3500000 km2 , 用科学记数法表示正确的是( )
A.3.5×105 km2
B.3.5×106 km2
C.3.5×107 km2
D.3.5×108 km2
查看答案和解析>>
科目:初中数学 来源: 题型:
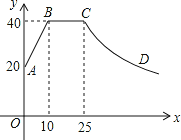
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为12米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).
(1)如何才能围成矩形花园的面积为75m2?
(2)能够围成面积为101m2的矩形花园吗?如能说明围法,如不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数L1:y=ax2﹣2ax+a+3(a>0)和二次函数L2:y=﹣a(x+1)2+1
(a>0)图象的顶点分别为M,N,与y轴分别交于点E,F.
(1)函数y=ax2﹣2ax+a+3(a>0)的最小值为______,当二次函数L1,L2的y值同时随着x的增大而减小时,x的取值范围是______.
(2)当EF=MN时,求a的值,并判断四边形ENFM的形状(直接写出,不必证明).
(3)若二次函数L2的图象与x轴的右交点为A(m,0),当△AMN为等腰三角形时,求方程﹣a(x+1)2+1=0的解.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com