
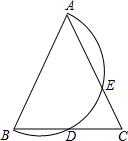
 已知:如图,在△ABC中,AB=AC,以腰AB为直径作半圆O,分别交BC,AC于点D,E.
已知:如图,在△ABC中,AB=AC,以腰AB为直径作半圆O,分别交BC,AC于点D,E.分析 (1)连接BE、AD,根据等腰三角形的性质即可得到结论;
(2)根据直径得出∠BEA=∠ADB=90°,求出∠ABE、∠DAB、∠DAC的度数,根据圆周角定理求出即可.
解答  解:连接BE、AD,
解:连接BE、AD,
∵AB是圆的直径,
∵AB=AC,
∴BD=CD,
∵AB是圆的直径,
∴∠ADB=∠AEB=90°,
∴∠ABE=90°-40°=50°,
AD⊥BC,
∵AB=AC,∠BAC=40°,
∴∠BAD=∠DAC=$\frac{1}{2}$∠BAC=20°,
∴由圆周角定理得:弧BD所对的圆心角的度数是2∠DAB=40°,
弧DE所对的圆心角的度数是2∠DAE=40°,
弧AE所对的圆心角的度数是2∠BAE=80°.
点评 题考查了圆周角定理,等腰三角形的性质的应用,主要考查了学生的推理能力和计算能力,注意:在同圆或等圆中,圆周角的度数等于它所夹弧所对的圆心角度数的一半.


科目:初中数学 来源: 题型:解答题
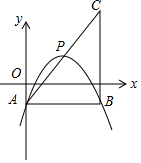 在平面直角坐标系中,已知抛物线y=-$\frac{1}{2}$x2+bx+c(b、c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),点C的坐标为(4,3)直角顶点B在第四象限.
在平面直角坐标系中,已知抛物线y=-$\frac{1}{2}$x2+bx+c(b、c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),点C的坐标为(4,3)直角顶点B在第四象限.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
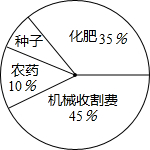 南县农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.南县农业部门对2014年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下统计表与统计图:
南县农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.南县农业部门对2014年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下统计表与统计图:| 每亩生产成本 | 每亩产量 | 油菜籽市场价格 | 种植面积 |
| 310元 | 130千克 | 5元/千克 | 500000亩 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com