
【题目】补全解答过程:
已知:如图,直线AB∥CD,直线EF与直线AB、CD分别交于点G、H,GM平分∠FGB,∠3=60°,求∠1的度数。

解:∵EF与CD交于点H(已知)
∴∠3=∠4(_______________)
∵∠3=60°(已知)
∴∠4=60°(______________)
∵AB∥CD,EF与AB、CD交于点G、H(已知)
∴∠4+∠FGB=180°(______________)
∴∠FGB=______°
∵GM平分∠FGB(已知)
∴∠1=_____°(______________)
【答案】对顶角相等;等量代换;两直线平行,同旁内角互补;120;60;角平分线的定义.
【解析】
依据对顶角相等以及平行线的性质,即可得到∠4=60°,∠FGB=120°,再根据角平分线的定义,即可得出∠1=60°.
解:∵EF与CD交于点H,(已知)
∴∠3=∠4.(对顶角相等)
∵∠3=60°,(已知)
∴∠4=60°.(等量代换)
∵AB∥CD,EF与AB,CD交于点G,H,(已知)
∴∠4+∠FGB=180°.(两直线平行,同旁内角互补)
∴∠FGB=120°.
∵GM平分∠FGB,(已知)
∴∠1=60°.(角平分线的定义)
故答案为:对顶角相等;等量代换;两直线平行,同旁内角互补;120;60;角平分线的定义.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD;
(2)若∠B=65°,∠EAC=25°,求∠AED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD顶点A、B在x轴上,点D在y轴上,函数y= ![]() (x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(x>0)的图象经过点C(2,3),直线AD交双曲线于点E,并且EB⊥x轴,CD⊥y轴,EB与CD交于点F.
(1)若EB= ![]() OD,求点E的坐标;
OD,求点E的坐标;
(2)若四边形ABCD为平行四边形,求过A、D两点的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,B、C、E三点共线,连接DC,点F为CD上的一点,连接AF.
(1)若BE平分∠AED,求证:AC=EC;
(2)若∠DAF=∠AEC,求证:BE=2AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:

(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
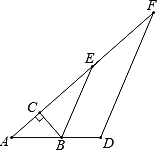
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.
(1)求∠CBE的度数;
(2)若∠F=25°,求证:BE∥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据![]() 单位:米
单位:米![]() ,解答下列问题:
,解答下列问题:
![]() 用含m,n的代数式表示地面的总面积S;
用含m,n的代数式表示地面的总面积S;
![]() 已知客厅面积是卫生间面积的8倍,且卫生间、卧室、厨房面积的和比客厅还少3平方米,如果铺1平方米地砖的平均费用为100元,那么小李铺地砖的总费用为多少元?
已知客厅面积是卫生间面积的8倍,且卫生间、卧室、厨房面积的和比客厅还少3平方米,如果铺1平方米地砖的平均费用为100元,那么小李铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
(1)根据如图2,写出一个代数恒等式: .
(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(3)小明同学用如图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a、b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z= .
(4)两个边长分别为a、b、c的直角三角形和一个两条直角边都是c的直角三角形拼成如图4.请你根据如图中图形的关系,写出一个代数恒等式,并写出推导过程.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,AB=3,点E在线段AB上,AE=1连结DE,DE的垂直平分线交DE于点P,交DC的延长线于点Q,PQ交BC于点G,连结EQ,EQ交BC于点F,连结GE.
(1)求证:△ADE∽△PQD;
(2)求线段CQ的长;
(3)求∠EGB的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com