

分析 由∠ACB=∠DEC=90°,∠A=45°,∠D=30°得到∠DCE=60°,△ABC为等腰直角三角形,再根据旋转的性质得∠D1CE1=∠DCE=60°∠BCE1=15°,所以∠D1CB=45°,于是可判断OC为等腰直角三角形ABC斜边上的中线,则OC⊥AB,OC=OA=$\frac{1}{2}$AB=3,则OD=CD-OC=4,然后在Rt△AOD1中根据勾股定理计算AD1.
解答 解:∵∠ACB=∠DEC=90°,∠A=45°,∠D=30°
∴∠DCE=60°,△ABC为等腰直角三角形,
∵三角板DCE绕着点C顺时针旋转15°得到△D1CE1,
∴∠D1CE1=∠DCE=60°∠BCE1=15°,
∴∠D1CB=45°,
∴OC平分∠ACB,
∴CO⊥AB,OA=OB,
∴OC=OA=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3,
∴OD=CD-OC=7-3=4,
在Rt△AOD1中,AD1=$\sqrt{A{O}^{2}+O{{D}_{1}}^{2}}$=5.
故答案为:5.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等腰直角三角形的性质和勾股定理.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{120}{x}$=$\frac{90}{35-x}$ | B. | $\frac{90}{x}$=$\frac{120}{35+x}$ | C. | $\frac{90}{3x}$=$\frac{120}{35}$ | D. | $\frac{90}{x}$=$\frac{120}{35-x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
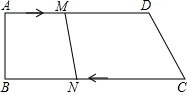 如图,已知四边形ABCD中,AD∥BC,∠B=90°,AD=25cm,CD=15cm,BC=35cm.动点M在AD边上以2cm/秒的速度由A向D运动;动点N在CB上以3cm/秒的速度由C向B运动,若点M,N分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,假设运动时间为t秒,问:
如图,已知四边形ABCD中,AD∥BC,∠B=90°,AD=25cm,CD=15cm,BC=35cm.动点M在AD边上以2cm/秒的速度由A向D运动;动点N在CB上以3cm/秒的速度由C向B运动,若点M,N分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,假设运动时间为t秒,问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
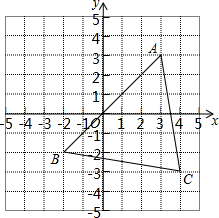 在如图所示的正方形网格中,每个小正方形的单位长度均为1,△ABC的三个顶点恰好是正方形网格的格点.
在如图所示的正方形网格中,每个小正方形的单位长度均为1,△ABC的三个顶点恰好是正方形网格的格点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
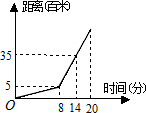 某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )
某天早上王文上学,先步行一段路,因时间紧,他又改乘出租车,结果到校时还是迟到了5分钟,其行程情况如图,若他出门时直接乘出租车(车速不变),则他( )| A. | 仍会迟到2分钟到校 | B. | 刚好按时到校 | ||
| C. | 可以提前2分钟到校 | D. | 可以提前5分钟到校 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>0 | B. | m>2 | C. | m<0 | D. | m<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com