
分析 (1)根据积的乘方和同底数幂的乘法可以解答本题;
(2)根据多项式乘多项式和平方差公式可以解答本题;
(3)根据同底数幂的除法和平方差公式可以解答本题;
(4)根据平方差公式和完全平方公式可以解答本题.
解答 解:(1)3a2b•${(-\frac{1}{2}{ab}^{2})}^{3}$
=$3{a}^{2}b•(-\frac{1}{8}){a}^{3}{b}^{6}$
=$-\frac{3}{8}{a}^{5}{b}^{7}$;
(2)(2a-3b)(a+b)-(a-2b)(a+2b)
=2a2+2ab-3ab-3b2-a2+4b2
=a2-ab+b2;
(3)(x-y)4÷(y-x)3•(y-x)
=(y-x)(y-x)
=y2-2xy+x2;
(4)(m-2n+3)(m+2n-3)
=[m-(2n-3)][m+(2n-3)]
=m2-(2n-3)2
=m2-4n2+12n-9;
点评 本题考查整式的混合运算,解答本题的关键是明确整式的混合运算的计算方法.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x y y y x x x x | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
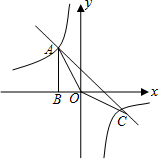 如图,点A(-1,m)是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点,另一个交点C在第四象限,AB⊥x轴于B,且cos∠AOB=$\frac{\sqrt{10}}{10}$
如图,点A(-1,m)是双曲线y1=$\frac{k}{x}$与直线y2=-x-(k+1)在第二象限的交点,另一个交点C在第四象限,AB⊥x轴于B,且cos∠AOB=$\frac{\sqrt{10}}{10}$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
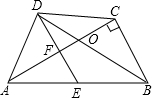 在四边形ABCD中,BD平分∠ABC,E为AB的中点,DE∥CB,∠ACB=90°,下面的结论中,正确的有①③④.①△BDE为等腰三角形,②∠AED=∠AOD,③AO•OC=DO•OB,④∠CAB=30°时,四边形BCDE为菱形.
在四边形ABCD中,BD平分∠ABC,E为AB的中点,DE∥CB,∠ACB=90°,下面的结论中,正确的有①③④.①△BDE为等腰三角形,②∠AED=∠AOD,③AO•OC=DO•OB,④∠CAB=30°时,四边形BCDE为菱形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com