
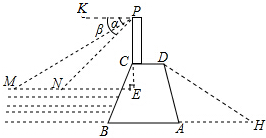
 某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD,大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD,大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.分析 (1)在直角△PEN,利用三角函数即可求得ME的长,根据MN=EM-EN求解;
(2)过点D作DN⊥AH于点N,利用三角函数求得AN和AH的长,进而求得△ADH的面积,得到需要填筑的土石方数,再根据结果比原计划提前20天完成,列方程求解.
解答 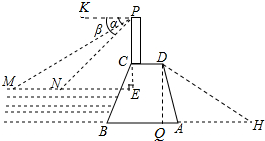 解:(1)在直角△PEN中,∠PNE=45°,
解:(1)在直角△PEN中,∠PNE=45°,
∴EN=PE=30m,
在Rt△PME中,∠PME=31°,
∴ME=$\frac{PE}{tan31°}$=50(m),
则MN=EM-EN=20(m).
答:两渔船M、N之间的距离是20米;
(2)过点D作DQ⊥AH于点Q.
由题意得:tan∠DAB=4,tanH=$\frac{4}{7}$,
在直角△DAQ中,AQ=$\frac{DQ}{tan∠DAB}$=$\frac{24}{4}$=6(m),
在直角△DHQ中,HQ=$\frac{DQ}{tanH}$=$\frac{24}{\frac{4}{7}}$=42(m).
故AH=HQ-AQ=42-6=36(m).
S△ADH=$\frac{1}{2}$AH•DQ=432(m2).
故需要填筑的土石方是V=SL=432×100=43200(m3).
设原计划平均每天填筑xm3,则原计划$\frac{43200}{x}$天完成,则增加机械设备后,现在平均每天填筑2xm3.
根据题意,得:10x+($\frac{43200}{x}-10-20$)•2x=43200,
解得:x=864.
经检验x=864是原方程的解.
答:施工队原计划平均每天填筑土石方864立方米.
点评 本题考查了仰角的定义以及坡度,要求学生能借助仰角构造直角三角形并解直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请用无刻度直尺在线段AB上画出点P,使AP=$\frac{2\sqrt{17}}{3}$,并保留作图痕迹.(备注:本题只是找点不是证明,∴只需连接一对角线就行)
如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请用无刻度直尺在线段AB上画出点P,使AP=$\frac{2\sqrt{17}}{3}$,并保留作图痕迹.(备注:本题只是找点不是证明,∴只需连接一对角线就行)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
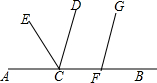 如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为90-$\frac{α}{2}$度(用关于α的代数式表示).
如图,点A,C,F,B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA为α度,则∠GFB为90-$\frac{α}{2}$度(用关于α的代数式表示).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
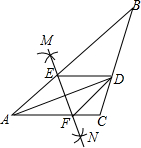 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com