
【题目】直线![]() 与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).

(1)求抛物线的解析式;
(2)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?
【答案】详见解析
【解析】
(1)首先求出点A,点C的坐标;然后利用待定系数法求出抛物线的解析式。
(2)AC为定值,当DE最大时,△ACD的面积最大,因此只需要求出△ACD面积的最大值即可。如图所示,作辅助线,利用S△ACD=S梯形AGFC﹣S△CDF﹣S△ADG求出S△ACD的表达式,然后利用二次函数的性质求出最大值,并进而求出点D的坐标和DE的最大值。
解:(1)在直线解析式![]() 中,令x=0,得y=﹣2;令y=0,得x=4,
中,令x=0,得y=﹣2;令y=0,得x=4,
∴A(4,0),C(0,﹣2)。
设抛物线的解析式为y=ax2+bx+c,
∵点A(4,0),B(1,0),C(0,﹣2)在抛物线上,
∴ ,解得
,解得 。
。
∴抛物线的解析式为:![]() 。
。
(2)设点D坐标为(x,y),![]() 。
。
在Rt△AOC中,OA=4,OC=2,由勾股定理得:AC=![]() 。
。
如图,连接CD、AD,过点D作DF⊥y轴于点F,过点A作AG⊥FD交FD的延长线于点G,

则FD=x,DG=4﹣x,OF=AG=y,FC=y+2。
S△ACD=S梯形AGFC﹣S△CDF﹣S△ADG
=![]() (AG+FC)FG﹣
(AG+FC)FG﹣![]() FCFD﹣
FCFD﹣![]() DGAG
DGAG
=![]() (y+y+2)×4﹣
(y+y+2)×4﹣![]() (y+2)x﹣
(y+2)x﹣![]() (4﹣x)y
(4﹣x)y
=2y﹣x﹣4
将![]() 代入得:S△ACD=2y﹣x﹣4=﹣x2+4x=﹣(x﹣2)2+4。
代入得:S△ACD=2y﹣x﹣4=﹣x2+4x=﹣(x﹣2)2+4。
∴当x=2时,△ACD的面积最大,最大值为4。
当x=2时,y=1,∴D(2,1)。
∵S△ACD=![]() ACDE,AC=
ACDE,AC=![]() ,
,
∴当△ACD的面积最大时,高DE最大,
则DE的最大值为: 。
。
∴当D与直线AC的距离DE最大时,点D的坐标为(2,1),最大距离为![]() 。
。


科目:初中数学 来源: 题型:
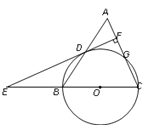
【题目】如图,等腰三角形ABC中,AC=BC=10,AB=12. 以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
(1)求证:直线EF是⊙O的切线;
(2)求sin∠E的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.
(1)求证:GE是⊙O的切线;
(2)若tanC=![]() ,BE=4,求AG的长.
,BE=4,求AG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
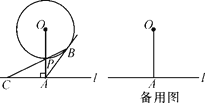
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为( )

A. 50m B. 100m C. 160m D. 200m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的![]() ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?
(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市开展早市促销活动,为早到的顾客准备一份简易早餐,餐品为四样A:菜包、B:面包、C:鸡蛋、D:油条.超市约定:随机发放,早餐一人一份,一份两样,一样一个.
(1)按约定,“某顾客在该天早餐得到两个鸡蛋”是 事件(填“随机”、“必然”或“不可能”);
(2)请用列表或画树状图的方法,求出某顾客该天早餐刚好得到菜包和油条的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
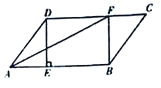
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
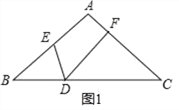
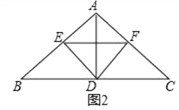
【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,求证:DECD=DFBE
(2)D为BC中点如图2,连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com