
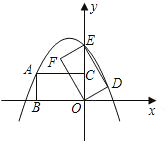
【题目】如图,在平面直角坐标系中,点O为坐标原点,点A在y轴的正半轴上,点B在x轴的负半轴上,点C是线段AB上一动点CD⊥y轴于点D,CE⊥x轴于点E,OA=6,AD=OE.
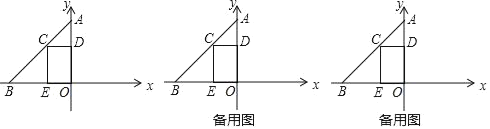
(1)求直线AB的解析式;
(2)连接ED,过点C作CF⊥ED,垂足为F,过点B作x轴的垂线交FC的延长线于点G,求点G的坐标;
(3)在(2)的条件下,连接AG,作四边形AOBG关于y轴的对称图形四边形AONM,连接DN,将线段DN绕点N逆时针旋转90°得到线段PN,H为OD中点,连接MH、PH,四边形MHPN的面积为40,连接FH,求线段FH的长.
【答案】(1)y=x+6;(2)G点坐标为(﹣6,6);(3)![]()
【解析】
(1)易证四边形DCEO为矩形,结合AD=OE,可得AD=CD,△ACD,△ABO是等腰直角三角形,OB=OA=6,从而获得A、B两点的坐标,然后用待定系数法就可以求出AB的解析式;
(2)可使用设参法,设D点坐标为(0,a),用(1)中的几何关系将OD、CE、AD、CD、EO表示出来,继而表示C、E点的坐标,用待定系数法求出直线DE的解析式,根据DE和FG的垂直关系以及C点的坐标求出直线FG的解析式,从而求出点G的坐标;
(3)设AD=a,通过已知的面积关系建立方程,求出a的值,从而获得各点的坐标,在△ADF中利用等面积法求出点F的坐标,从而求出FH的长.
解:(1)∵CD⊥y轴,CE⊥x轴
∴∠CDO=∠CEO=90°
又∵∠DOE=90°
∴四边形DCEO是矩形
∴CD=OE
又∵AD=OE
∴AD=CE
∴AD=CD
∴△ACD是等腰直角三角形
∴∠ACD=45°
∴∠ABO=45°
∴∠ACD=∠ABO
∴AO=BO=6
∴A(0,6),B(﹣6,0)
设直线AB的解析式为y=kx+6
将A(﹣6,0)代入,得0=﹣6k+6
解得,k=1
∴直线AB的解析式为:y=x+6
(2)
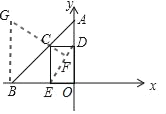
如图所示,设D(0,a),则OD=CE=a,AD=CD=EO=6﹣a
∴C(a﹣6,a),E(a﹣6,0)
设yDE=k1x+a,将E(a﹣6,0)代入,得,
0=(a﹣6)k1+a
解得,![]()
∴yDE=![]()
设yFG=k2x+b1
∵DE⊥FG
∴k1k2=﹣1
∴![]()
∴yFG=![]()
将C(a﹣6,a)代入,得,![]()
解得,![]()
∴yFG=![]() +
+![]()
∵当x=﹣6时,yFG=6
∴G点坐标为(﹣6,6)
(3)根据题意,如图所示
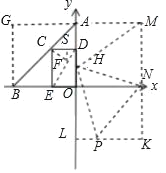
可证△ODN≌△NPK
∴ON=NK=6
∴四边形ONKL为正方形
设AD=a,则OH=DH=3﹣![]()
PK=OD=6﹣a
LP=a
SMHPN=SAMKL﹣S△AMH﹣S△NKP﹣S△OLP
=6×12﹣![]()
=45﹣3a+![]()
45﹣3a+![]() =40
=40
解得a1=2,a2=10(舍)
作FS⊥CD
可得CD=2,EC=4
∴ED=2![]()
由等面积法
CDCE=EDCF
2×4=2![]() ×CF
×CF
∴CF=![]()
∵CD=2
∴DF=![]()
CDFS=CFFD
FS=![]()
∴SD=![]()
∴F(![]() ,
,![]() )
)
∴![]()


科目:初中数学 来源: 题型:
【题目】为了解七年级学生身体发育状况,学校抽取一部分学生测量身高(单位:m),绘制处如下的统计图①和图②.请根据相关信息,解答下列问题:
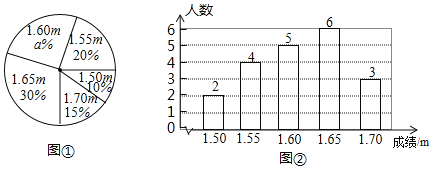
(1)图①中a的值为 ;
(2)求统计的这组学生身高数据的平均数、众数和中位数;
(3)如果全校七年级学生有300人,那么估计身高大于1.65m的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0)和B(m,0),且3<m<4,则下列说法:①b<0;②a+c=b;③b2>4ac;④2b>3c;⑤![]() =1,正确的是( )
=1,正确的是( )
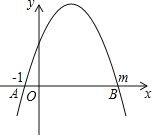
A.①②④B.①③⑤C.②③④D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
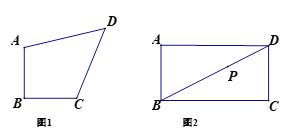
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,则对角线BD的长为 ;
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点![]() 是对角线
是对角线![]() 上一点,且
上一点,且![]() ,过点
,过点![]() 作直线分别交边
作直线分别交边![]() 于点
于点![]() ,使四边形
,使四边形![]() 是等腰直角四边形.直接写出
是等腰直角四边形.直接写出![]() 的长为 .
的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
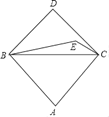
【题目】如图,在△ABC中,AB=AC,以BC为斜边作等腰直角三角形BCD,E是△BCD内一点,连接BE和EC,BE=AB,∠BEC+![]() ∠BAC=180°.若EC=1,tan∠ABC=
∠BAC=180°.若EC=1,tan∠ABC=![]() ,则线段BD的长是_____.
,则线段BD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
(1)收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=______,n=______.
(3)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 72 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=______,y=______.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有______人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
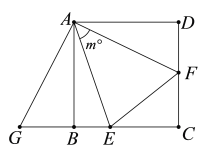
【题目】如图,已知正方形![]() 的边长是
的边长是![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() 于点
于点![]() ,
,![]() 是
是![]() 延长线上一点,且始终保持
延长线上一点,且始终保持![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)当![]() 时:
时:
①求![]() 的值;②若
的值;②若![]() 是
是![]() 的中点,求
的中点,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知抛物线y=ax2-2x+c与直线y=kx+b都经过A(0,-3)、B(3,0)两点,该抛物线的顶点为C.
(1)求此抛物线和直线AB的解析式;
(2)设直线AB与该抛物线的对称轴交于点E,在射线EB上是否存在一点M,过M作x轴的垂线交抛物线于点N,使点M、N、C、E是平行四边形的四个顶点?若存在,求点M的坐标;若不存在,请说明理由;
(3)设点P是直线AB下方抛物线上的一动点,当△PAB面积最大时,求点P的坐标,并求△PAB面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1,OB=![]() ,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
,矩形ABOC绕点O按顺时针方向旋转60°后得到矩形EFOD.点A的对应点为点E,点B的对应点为点F,点C的对应点为点D,抛物线y=ax2+bx+c过点A,E,D.
(1)判断点E是否在y轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在x轴的上方是否存在点P,点Q,使以点O,B,P,Q为顶点的平行四边形的面积是矩形ABOC面积的2倍,且点P在抛物线上?若存在,请求出点P,点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com