
| AB |
| AD |
| AE |
| AF |
| AE |
| AF |
| AM |
| AD |
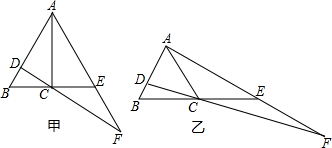
 解:(1)△CBD∽△FAD;理由如下:
解:(1)△CBD∽△FAD;理由如下:| AE |
| AF |
| AM |
| AD |
| AB |
| AD |
| AE |
| AF |
| 2λ+μ |
| λ+μ |
| μ |
| λ+μ |
| 2(λ+μ) |
| λ+μ |
| AB |
| AD |
| AE |
| AF |


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
 如图,直线AB分别与两坐标轴交于点A(8,0)、B(0,6).
如图,直线AB分别与两坐标轴交于点A(8,0)、B(0,6).查看答案和解析>>
科目:初中数学 来源: 题型:
| A、对全国中学生心理健康现状的调查 |
| B、对冷饮市场上冰淇淋质量情况的调查 |
| C、对西安市市民实施低碳生活情况的调查 |
| D、对“神舟九号”飞船零部件状况的检查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com