
科目:初中数学 来源: 题型:解答题
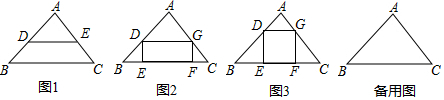
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
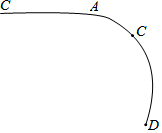 如图,一段圆弧AB上有一个点D,直线AC与圆弧相切于点A,请借助于切点A及B、D两点,利用尺规作图找出这段圆弧所在圆的圆心(不写作法,保留作图痕迹).
如图,一段圆弧AB上有一个点D,直线AC与圆弧相切于点A,请借助于切点A及B、D两点,利用尺规作图找出这段圆弧所在圆的圆心(不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
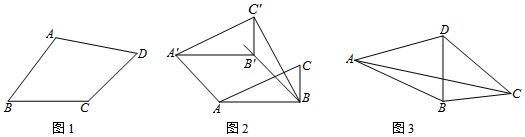
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
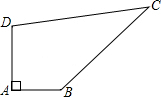 如图,某开发区计划在一块四边形的空地ABCD上种植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,种植每平方米草皮的预算费用为300元,若第一年对草坪的保养费用占种植草皮总预算的4%,以后每年的保养费用都将在前一年的基础上递增2%,求第三年的草坪保养费用.
如图,某开发区计划在一块四边形的空地ABCD上种植草坪,已知∠A=90°,AB=4m,BC=12m,CD=13m,DA=3m,种植每平方米草皮的预算费用为300元,若第一年对草坪的保养费用占种植草皮总预算的4%,以后每年的保养费用都将在前一年的基础上递增2%,求第三年的草坪保养费用.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com