
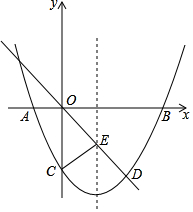
 如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).分析 (1)利用待定系数法求抛物线的函数表达式和直线DE的解析式,利用配方法求抛物线的对称轴,即点E的横坐标为x=3,代入直线DE中可求得E的纵坐标,根据对称性求得点B的坐标;
(2)如图1,根据△FOE≌△FCE,对应边相等,得FC=FO,所以F在OC的中垂线上,点F纵坐标为-4,代入抛物线后求得点F的坐标;
(3)由题意可知:分情况讨论:即当OP=OQ和当OQ=PQ时,△OPQ是等腰三角形,构建平行线,利用相似三角形的性质和判定,结合待定系数法解一次函数的解析式,即可求出结论;
(4)如图4中,取点K(0,-2),连接BK、KF′、OF′,只要证明△KOF′∽△F′OC,推出KF′=$\frac{1}{2}$F′C,所以2BF′+CF′=2(BF′+$\frac{1}{2}$CF′)≥2BK,所以当K、F′、B共线时,2BF′+CF′的值最小,最小值为2BK.
解答 解:(1)∵抛物线y=ax2+bx-8经过点A(-2,0),D(6,-8),
∴$\left\{\begin{array}{l}{4a-2b-8=0}\\{36a+6b-8=-8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-3}\end{array}\right.$,
∴抛物线解析式为y=$\frac{1}{2}$x2-3x-8,
∵y=$\frac{1}{2}$x2-3x-8=$\frac{1}{2}$(x-3)2-$\frac{25}{2}$,
∴抛物线对称轴为直线x=3,
又∵抛物线与x轴交于点A、B两点,点A坐标(-2,0),
∴点B坐标(8,0).
设直线l的解析式为y=kx,
∵经过点D(6,-8),
∴6k=-8,
∴k=-$\frac{4}{3}$,
∴直线l的解析式为y=-$\frac{4}{3}$x,
∵点E为直线l与抛物线的交点,
∴点E的横坐标为3,纵坐标为-$\frac{4}{3}$×3=-4,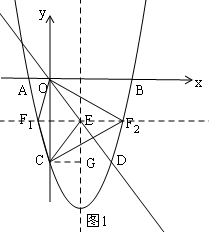
∴点E坐标(3,-4).
(2)如图1,抛物线上存在点F使得△FOE≌△FCE,
过C作CG⊥对称轴于G,
当x=0时,y=-8,
∴C(0,-8),
∴OC=8,
∵E(3,-4),
由勾股定理得:OE=5,CE=5,
∴OE=CE,
此时点F纵坐标为-4,
∴$\frac{1}{2}$x2-3x-8=-4,
∴x2-6x-8=0,
x=3±$\sqrt{17}$,
∴点F坐标(3+$\sqrt{17}$,-4)或(3-$\sqrt{17}$,-4);
(3)①如图2中,当OP=OQ时,△OPQ是等腰三角形.
∵点E坐标(3,-4),
∴OE=$\sqrt{{3}^{2}+{4}^{2}}$=5,过点E作直线ME∥PB,交y轴于点M,交x轴于点H.则$\frac{OM}{OP}$=$\frac{OE}{OQ}$,
∴OM=OE=5,
∴点M坐标(0,-5).
设直线ME的解析式为y=k1x-5,
∴3k1-5=-4,
∴k1=$\frac{1}{3}$,
∴直线ME解析式为y=$\frac{1}{3}$x-5,
令y=0,得$\frac{1}{3}$x-5=0,解得x=15,
∴点H坐标(15,0),
∵MH∥PB,
∴$\frac{OP}{OM}$=$\frac{OB}{OH}$,即$\frac{-m}{5}$=$\frac{8}{15}$,
∴m=-$\frac{8}{3}$,
②如图3,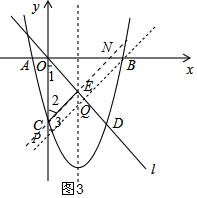
当QO=QP时,△POQ是等腰三角形.
由(2)得OE=CE,
∴∠1=∠2,
∵QO=QP,
∴∠1=∠3,
∴∠2=∠3,
∴CE∥PB,
设直线CE交x轴于N,解析式为y=k2x-8,
∴3k2-8=-4,
∴k2=$\frac{4}{3}$,
∴直线CE解析式为y=$\frac{4}{3}$x-8,
令y=0,得$\frac{4}{3}$x-8=0,
∴x=6,
∴点N坐标(6,0),
∵CN∥PB,
∴$\frac{OP}{OC}$=$\frac{OB}{ON}$,
∴$\frac{-m}{8}$=$\frac{8}{6}$,
∴m=-$\frac{32}{3}$.
③OP=PQ时,显然不可能,理由,
∵D(6,-8),
∴∠1<∠BOD,
∵∠OQP=∠BOQ+∠ABP,
∴∠PQO>∠1,
∴OP≠PQ,
综上所述,当m=-$\frac{8}{3}$或-$\frac{32}{3}$时,△OPQ是等腰三角形;
(4)如图4中,取点K(0,-2),连接BK、KF′、OF′.
∵∠KOF′=∠COF′,OK=2,OF′=4,OC=OB=8,
∴$\frac{OK}{OF′}$=$\frac{OF′}{OC}$=$\frac{1}{2}$,
∴△KOF′∽△F′OC,
∴KF′=$\frac{1}{2}$F′C,
∴2BF′+CF′=2(BF′+$\frac{1}{2}$CF′)≥2BK,
∴当K、F′、B共线时,2BF′+CF′的值最小,最小值为2BK=2•$\sqrt{{8}^{2}+{2}^{2}}$=4$\sqrt{17}$.
点评 本题是二次函数的综合题,考查了一次函数的性质、待定系数法、等腰三角形的性质和判定等知识,解题的关键是学会分类讨论,注意不能漏解,与方程相结合,本题构造相似三角形解决最值问题是难点,属于中考压轴题..


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:选择题
| A. | 单项式x没有系数 | B. | mn2与-$\frac{1}{2}$n2m是同类项 | ||
| C. | 3x3y的次数是3 | D. | 多项式3x-1的项是3x和1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
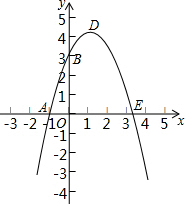 已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.
已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
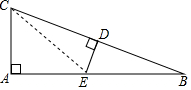 如图,在 Rt△ABC 中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )
如图,在 Rt△ABC 中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )| A. | 4cm | B. | 8cm | C. | 16cm | D. | 32cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com