
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如果小球在如图所示的七巧板上自由滚动,并随机停留在这七巧板的某个位置上(不考虑停在边线的情况),那么它最终停留在四边形EFLH的概率是$\frac{1}{8}$.
如果小球在如图所示的七巧板上自由滚动,并随机停留在这七巧板的某个位置上(不考虑停在边线的情况),那么它最终停留在四边形EFLH的概率是$\frac{1}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
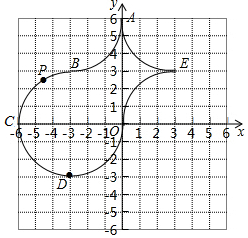 如图,在平面直角坐标系xOy中,几段$\frac{1}{4}$圆弧(占圆周的$\frac{1}{4}$的圆弧)首尾连接围成的封闭区域形如“宝瓶”,其中圆弧连接点都在正方形网格的格点处,点A的坐标是A(0,6),点C的坐标是C(-6,0).
如图,在平面直角坐标系xOy中,几段$\frac{1}{4}$圆弧(占圆周的$\frac{1}{4}$的圆弧)首尾连接围成的封闭区域形如“宝瓶”,其中圆弧连接点都在正方形网格的格点处,点A的坐标是A(0,6),点C的坐标是C(-6,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
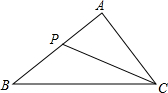 如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件,错误的是( )
如图,点P在△ABC的边AB上,要判断△ACP∽△ABC,添加一个条件,错误的是( )| A. | ∠ACP=∠B | B. | ∠APC=∠ACB | C. | $\frac{AP}{AC}$=$\frac{AC}{AB}$ | D. | $\frac{AC}{CP}$=$\frac{AB}{BC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 △ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,则下列说法错误的是( )
△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,则下列说法错误的是( )| A. | 四边形ABED是矩形 | B. | AD${\;}_{=}^{∥}$CF | ||
| C. | BC=CF | D. | DF=CF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com