
 ×ß½ųĪÄŃŌĪÄĻµĮŠ“š°ø
×ß½ųĪÄŃŌĪÄĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | Õż·½ŠĪ | B£® | ¾ŲŠĪ | C£® | ĮāŠĪ | D£® | Ö±½ĒĢŻŠĪ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼ĖłŹ¾£¬ŌŚĆæøö±ß³¤¶¼ĪŖ1µÄŠ”Õż·½ŠĪ×é³ÉµÄĶųøńÖŠ£¬µćA”¢B”¢C¾łĪŖøńµć£®
ČēĶ¼ĖłŹ¾£¬ŌŚĆæøö±ß³¤¶¼ĪŖ1µÄŠ”Õż·½ŠĪ×é³ÉµÄĶųøńÖŠ£¬µćA”¢B”¢C¾łĪŖøńµć£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬”÷APBCŹĒµČ±ßČż½ĒŠĪ£¬Į¬½ÓPD£¬DB£¬Ōņ$\frac{{S}_{”÷BPD}}{{S}_{Õż·½ŠĪABCD}}$=$\frac{\sqrt{3}-1}{4}$£®
ČēĶ¼£¬ŌŚÕż·½ŠĪABCDÖŠ£¬”÷APBCŹĒµČ±ßČż½ĒŠĪ£¬Į¬½ÓPD£¬DB£¬Ōņ$\frac{{S}_{”÷BPD}}{{S}_{Õż·½ŠĪABCD}}$=$\frac{\sqrt{3}-1}{4}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
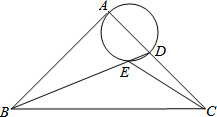 ČēĶ¼£¬ŌŚµČŃüÖ±½Ē”÷ABCÖŠ£¬”ĻBAC=90”ć£¬AB=AC£¬BC=4$\sqrt{2}$£¬µćDŹĒACÉĻŅ»¶Æµć£¬Į¬½ÓBD£¬ŅŌADĪŖÖ±¾¶µÄŌ²½»BDÓŚµćE£¬ŌņĻ߶ĪCE³¤¶ČµÄ×īŠ”ÖµŹĒ£Ø””””£©
ČēĶ¼£¬ŌŚµČŃüÖ±½Ē”÷ABCÖŠ£¬”ĻBAC=90”ć£¬AB=AC£¬BC=4$\sqrt{2}$£¬µćDŹĒACÉĻŅ»¶Æµć£¬Į¬½ÓBD£¬ŅŌADĪŖÖ±¾¶µÄŌ²½»BDÓŚµćE£¬ŌņĻ߶ĪCE³¤¶ČµÄ×īŠ”ÖµŹĒ£Ø””””£©| A£® | 2 | B£® | 4 | C£® | $2\sqrt{2}-2$ | D£® | $2\sqrt{5}-2$ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Å×ĪļĻßy=$\frac{1}{4}$x2+bx+c¾¹żµćA£Ø-2£¬0£©ŗĶŌµć£¬µćBŌŚÅ×ĪļĻßÉĻĒŅtan”ĻBAO=$\frac{1}{2}$£¬Å×ĪļĻߵĶŌ³ĘÖįÓėxÖįĻą½»ÓŚµćP£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Å×ĪļĻßy=$\frac{1}{4}$x2+bx+c¾¹żµćA£Ø-2£¬0£©ŗĶŌµć£¬µćBŌŚÅ×ĪļĻßÉĻĒŅtan”ĻBAO=$\frac{1}{2}$£¬Å×ĪļĻߵĶŌ³ĘÖįÓėxÖįĻą½»ÓŚµćP£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com