
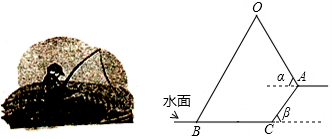
分析 (1)作OD⊥BC于D,AF⊥BC于F,AE⊥OD于E,根据正弦的概念求出AF、CF、OE,结合图形计算;
(2)根据正切的概念求出BD,根据BC=BD+AE-CF计算.
解答 解:(1)作OD⊥BC于D,AF⊥BC于F,AE⊥OD于E,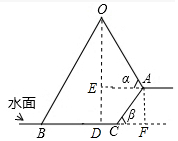
∵河堤AC的坡角β为45°,
∴AF=CF=AC×sin∠ACF=$\sqrt{2}$,
∵钓竿OA的倾斜角α为60°,
∴OE=OA×sin∠OAE=2$\sqrt{3}$,AE=2,
则OD=OE+DE=OE+AF=$\sqrt{2}$+2$\sqrt{3}$,
答:点O到水面的垂直距离为($\sqrt{2}$+2$\sqrt{3}$)米;
(2)由题意得,∠BOD=30°,
∴BD=OD×tan30°=$\frac{\sqrt{6}}{3}$+2,
∴BC=BD+AE-CF=$\frac{\sqrt{6}}{3}$+4-$\sqrt{2}$,
答:浮漂B与河堤点C之间的距离为($\frac{\sqrt{6}}{3}$+4-$\sqrt{2}$)米.
点评 本题考查的是解直角三角形的应-坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的概念是解题的关键.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:填空题
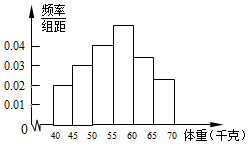 为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为1500人.
为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为1500人.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 0,-1或1 | C. | 1或-1 | D. | 0或1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
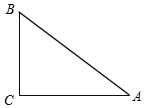 在Rt△ABC中,∠C=90°,AC=4,BC=3,
在Rt△ABC中,∠C=90°,AC=4,BC=3,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com