


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
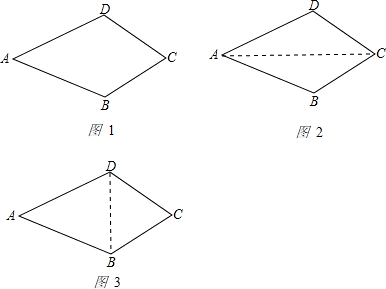
在一堂数学课中,数学老师给出了如下问题“已知:如图①,在四边形ABCD中,AB=AD,∠B=∠D.求证:CB=CD”.文文和彬彬都想到了利用辅助线把四边形的问题转化为三角形来解决.
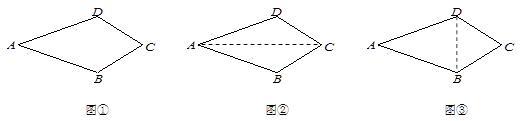 |
(1)文文同学证明过程如下:连结AC(如图②)
∵∠B=∠D ,AB=AD,AC=AC
∴△ABC≌△ADC,∴CB=CD
你认为文文的证法是 的.(在横线上填写“正确”或“错误”)
(2)彬彬同学的辅助线作法是“连结BD”(如图③),请完成彬彬同学的证明过程.
查看答案和解析>>
科目:初中数学 来源:2012年内蒙古赤峰市升学、毕业统一考试模拟数学试卷 题型:解答题
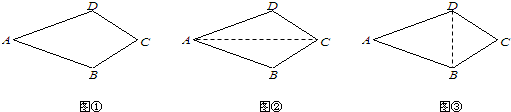
在一堂数学课中,数学老师给出了如下问题“已知:如图①,在四边形ABCD中,AB=AD,∠B=∠D.求证:CB=CD”.文文和彬彬都想到了利用辅助线把四边形的问题转化为三角形来解决.
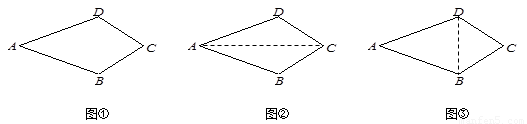
1.文文同学证明过程如下:连结AC(如图②)
∵∠B=∠D ,AB=AD,AC=AC
∴△ABC≌△ADC,∴CB=CD
你认为文文的证法是 的.(在横线上填写“正确”或“错误”)
2.彬彬同学的辅助线作法是“连结BD”(如图③),请完成彬彬同学的证明过程.
查看答案和解析>>
科目:初中数学 来源:2011年内蒙古九年级第二次模拟考试数学卷 题型:解答题
(本题10分)在一堂数学课中,数学老师给出了如下问题“已知:如图①,在四边形ABCD中,AB=AD,∠B=∠D.求证:CB=CD”.文文和彬彬都想到了利用辅助线把四边形的问题转化为三角形来解决.

1.(1)文文同学证明过程如下:连结AC(如图②)
∵∠B=∠D ,AB=AD,AC=AC
∴△ABC≌△ADC,∴CB=CD
你认为文文的证法是 的.(在横线上填写“正确”或“错误”)
2.(2)彬彬同学的辅助线作法是“连结BD”(如图③),请完成彬彬同学的证明过程.
查看答案和解析>>
科目:初中数学 来源:2010-2011学年山东肥城马埠中学毕业班数学月考试卷(四) 题型:解答题
在一堂数学课中,数学老师给出了如下问题“已知:如图①,在四边形ABCD中,AB=AD,∠B=∠D.求证:CB=CD”.文文和彬彬都想到了利用辅助线把四边形的问题转化为三角形来解决.
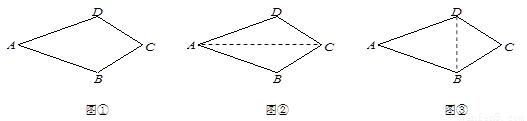
1.文文同学证明过程如下:连结AC(如图②)
∵∠B=∠D ,AB=AD,AC=AC
∴△ABC≌△ADC,∴CB=CD
你认为文文的证法是 的.(在横线上填写“正确”或“错误”)
2.彬彬同学的辅助线作法是“连结BD”(如图③),请完成彬彬同学的证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com