
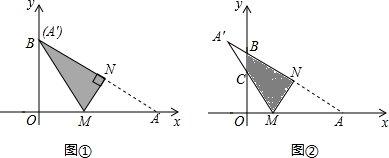
分析 (Ⅰ)根据折叠的性质得出BM=AM,再由勾股定理进行解答即可;
(Ⅱ)根据勾股定理和三角形的面积得出△AMN,△COM和△ABO的面积,进而表示出S的代数式即可;
(Ⅲ)把S=$\frac{\sqrt{3}}{24}$代入解答即可.
解答 解:(Ⅰ)在Rt△ABO中,点A($\sqrt{3}$,0),点B(0,1),点O(0,0),
∴OA=$\sqrt{3}$,OB=1,
由OM=m,可得:AM=OA-OM=$\sqrt{3}$-m,
根据题意,由折叠可知△BMN≌△AMN,
∴BM=AM=$\sqrt{3}$-m,
在Rt△MOB中,由勾股定理,BM2=OB2+OM2,
可得:$(\sqrt{3}-m)^{2}=1+{m}^{2}$,解得m=$\frac{\sqrt{3}}{3}$,
∴点M的坐标为($\frac{\sqrt{3}}{3}$,0);
(Ⅱ)在Rt△ABO中,tan∠OAB=$\frac{OB}{OA}=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$,
∴∠OAB=30°,
由MN⊥AB,可得:∠MNA=90°,
∴在Rt△AMN中,MN=AM•sin∠OAB=$\frac{1}{2}(\sqrt{3}-m)$,
AN=AN•cos∠OAB=$\frac{\sqrt{3}}{2}(\sqrt{3}-m)$,
∴${S}_{△AMN}=\frac{1}{2}MN•AN=\frac{\sqrt{3}}{8}(\sqrt{3}-m)^{2}$,
由折叠可知△A'MN≌△AMN,则∠A'=∠OAB=30°,
∴∠A'MO=∠A'+∠OAB=60°,
∴在Rt△COM中,可得CO=OM•tan∠A'MO=$\sqrt{3}$m,
∴${S}_{△COM}=\frac{1}{2}OM•CO=\frac{\sqrt{3}}{2}{m}^{2}$,
∵${S}_{△ABO}=\frac{1}{2}OA•OB=\frac{\sqrt{3}}{2}$,
∴$S={S}_{△ABO}-{S}_{△AMN}-{S}_{△COM}=\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{8}(\sqrt{3}-m)^{2}-\frac{\sqrt{3}}{2}{m}^{2}$,
即$S=-\frac{5\sqrt{3}}{8}{m}^{2}+\frac{3}{4}m+\frac{\sqrt{3}}{8}(0<m<\frac{\sqrt{3}}{3})$;
(Ⅲ)①当点A′落在第二象限时,把S的值代入(2)中的函数关系式中,解方程求得m,根据m的取值范围判断取舍,两个根都舍去了;
②当点A′落在第一象限时,则S=SRt△AMN,根据(2)中Rt△AMN的面积列方程求解,根据此时m的取值范围,把S=$\frac{\sqrt{3}}{24}$代入,可得点M的坐标为($\frac{2\sqrt{3}}{3}$,0).
点评 此题考查了一次函数的综合问题,关键是利用勾股定理、三角形的面积,三角函数的运用进行分析.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位s)关系的函数图象中,正确的是( )
如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位s)关系的函数图象中,正确的是( )| A. | 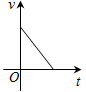 | B. | 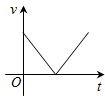 | C. | 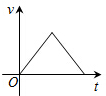 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{500}{x+30}=\frac{350}{x}$ | B. | $\frac{500}{x-30}=\frac{350}{x}$ | C. | $\frac{500}{x}=\frac{350}{x-30}$ | D. | $\frac{500}{x}=\frac{350}{x+30}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 ,
,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=-x2-2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=$\frac{1}{2}$x-a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.
已知抛物线y=-x2-2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=$\frac{1}{2}$x-a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是720米.
如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是720米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com