
分析 (1)首先根据x2=$\frac{{x}_{1}+{x}_{3}}{2}$,可得x3=2x2-x1,据此求出x3是多少;然后根据x3=$\frac{{x}_{2}{+x}_{4}}{2}$,求出x4是多少;最后根据${x}_{4}=\frac{{x}_{3}{+x}_{5}}{2}$,求出x5是多少即可;
(2)根据x1=1=3×1-1,x2=4=3×2-2,…,猜想第k个数xk=3k-2,然后把k=2013代入,求出x2013是多少即可.
解答 解:(1)因为x2=$\frac{{x}_{1}+{x}_{3}}{2}$,
所以x3=2x2-x1=2×4-1=7;
因为x3=$\frac{{x}_{2}{+x}_{4}}{2}$,
所以x4=2x3-x2=2×7-4=10;
因为${x}_{4}=\frac{{x}_{3}{+x}_{5}}{2}$,
所以x5=2x4-x3=2×10-7=13.
即第三个数是7,第四个数是10,第五个数是13.
(2)因为x1=1=3×1-1,x2=4=3×2-2,x3=7=3×3-2,x4=10=3×4-2,…,
所以猜想第k个数xk=3k-2,
所以x2013=3×2013-2=6037.
点评 (1)此题主要考查了探寻数字规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:第k个数xk=3k-2.
(2)此题还考查了分析推理能力的应用,解答此题的关键是判断出相邻两个数的差都是3.


科目:初中数学 来源: 题型:填空题
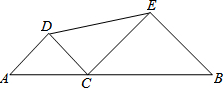 如图,线段AB的长为10,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角△ACD和△BCE,那么DE长的最小值是5.
如图,线段AB的长为10,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角△ACD和△BCE,那么DE长的最小值是5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
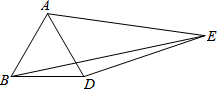 如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )
如图,△ABD是等边三角形,以AD为边向外作△ADE,使∠AED=30°,且AE=3,DE=2,连接BE,则BE的长为( )| A. | 4 | B. | $\sqrt{13}$ | C. | 5 | D. | $\sqrt{15}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com