
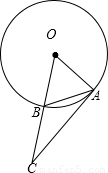
如图,已知弦AB等于半径,连结OB并延长使BC=OB.
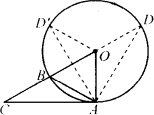
(1)求证:AC是⊙O的切线;
(2)请你在⊙O上选取一点D,使得AD=AC.
|
(1)∵AB=OB=BC, ∴∠CAB=∠ACB= ∴∠OAC=∠OAB+∠CAB=60°+30°=90°,即OA⊥CA, ∴AC是⊙O的切线. (2)可作BO的延长线交⊙O于D,连结AD, ∴CB=BO=OD,又有AB=AO,∠CBA=180°-∠ABO=180°-∠BOA=∠AOD, ∴△AOD≌△ABC,∴AD=AC, 故点D即为所求. 另外,在圆上取一点 |
|
证明一条直线是圆的切线,通常选择:(1)到圆心的距离等于圆的半径的直线是圆的切线;(2)经过半径的外端并且垂直于这条半径的直线是圆的切线.而涉及切线问题时,应灵活运用切线的性质,通常连结切点圆心:“遇到切线连切点,用好性质是关键”. |


科目:初中数学 来源: 题型:
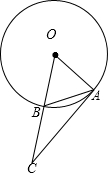 如图,已知弦AB等于半径,连接OB并延长使BC=OB.
如图,已知弦AB等于半径,连接OB并延长使BC=OB.查看答案和解析>>
科目:初中数学 来源:2009-2010学年山东省滨州市无棣县第二实验学校九年级(上)期末数学模拟试卷(2)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2000年陕西省中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2000年全国中考数学试题汇编《圆》(06)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com