
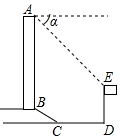
 如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,求大楼AB的高度是多少?(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45)
如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:$\sqrt{3}$,求大楼AB的高度是多少?(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{6}$≈2.45) 分析 延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,设BH=x米,则CH=$\sqrt{3}$x米,在Rt△BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6$\sqrt{3}$米,得出BG、EG的长度,证明△AEG是等腰直角三角形,得出AG=EG=6$\sqrt{3}$+20(米),即可得出大楼AB的高度.
解答 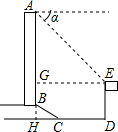 解:延长AB交DC于H,作EG⊥AB于G,如图所示:
解:延长AB交DC于H,作EG⊥AB于G,如图所示:
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1:$\sqrt{3}$,
∴BH:CH=1:$\sqrt{3}$,
设BH=x米,则CH=$\sqrt{3}$x米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+($\sqrt{3}$x)2=122,
解得:x=6,
∴BH=6米,CH=6$\sqrt{3}$米,
∴BG=GH-BH=15-6=9(米),EG=DH=CH+CD=6$\sqrt{3}$+20(米),
∵∠α=45°,
∴∠EAG=90°-45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=6$\sqrt{3}$+20(米),
∴AB=AG+BG=6$\sqrt{3}$+20+9≈39.4(米).
故大楼AB的高度大约是39.4米.
点评 本题考查了解直角三角形的应用-坡度、俯角问题;通过作辅助线运用勾股定理求出BH,得出EG是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 对顶角相等 | |
| B. | 角平分线上的点到这个角的两边的距离相等 | |
| C. | 如果a2=b2,那么a=b | |
| D. | 同旁内角互补,两直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个.
某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多17个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)解不等式组:$\left\{\begin{array}{l}{3x+1≤2}\\{\frac{2x-1}{3}>x}\end{array}\right.$
(1)解不等式组:$\left\{\begin{array}{l}{3x+1≤2}\\{\frac{2x-1}{3}>x}\end{array}\right.$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
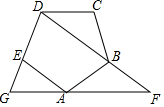
 如图,菱形ABCD中,∠BAD=45°,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于2,则AB=2$\sqrt{2}$.
如图,菱形ABCD中,∠BAD=45°,E,F,P分别是AB,BC,AC上的动点,PE+PF的最小值等于2,则AB=2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
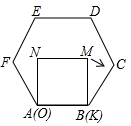 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:| A. | 1.4 | B. | 1.1 | C. | 0.8 | D. | 0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com