练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，我们可以用下面的方法测出月球与地球的距离：在月圆时，把一个五分的硬币(直径约为2.4cm)放在离眼睛O约1.44m的AB处，正好把月亮遮住，已知月球的直径约为3500km，你能算出月球与地球的距离吗？(保留两位有效数字)

    答案：
    解析：

    　　AB∥CD　　∴△OAB∽△OCD　　又∴OE⊥AB，OF⊥CD　　∴＝且AB＝2.4cm　　CD＝350000000cm

    　　OE＝2m　　∴OF＝·CD＝×350000000＝210000000(m)＝2.1×108(m)＝2.1×105(km)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

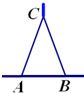    精英家教网精英家教网小知识：如图，我们称两臂长度相等（即CA=CB）的圆规为等臂圆规．当等臂圆规的两脚摆放在一条直线上时，若张角∠ACB=x°，则底角∠CAB=∠CBA=（90-
    x2
    ）°．
    请运用上述知识解决问题：如图，n个相同规格的等臂圆规的两脚依次摆放在同一条直线上，其张角度数变化如下：∠A1C1A2=160°，∠A2C2A3=80°，∠A3C3A4=40°，∠A4C4A5=20°，…
    精英家教网
    （1）①由题意可得∠A1A2C1=
     
    °；
    ②若A2M平分∠A3A2C1，则∠MA2C2=
     
    °；
    （2）∠An+1AnCn=
     
    °（用含n的代数式表示）；
    （3）当n≥3时，设∠An-1AnCn-1的度数为a，∠An+1AnCn-1的角平分线AnN与AnCn构成的角的度数为β，那么a与β之间的等量关系是
     
    ，请说明理由．（提示：可以借助下面的局部示意图）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图①，我们在“格点”直角坐标系上可以清楚看到：要找AB或DE的长度，显然是转化为求Rt△ABC或Rt△DEF的斜边长．

    下面：以求DE为例来说明如何解决：
    从坐标系中发现：D（-7，5），E（4，-3）．所以DF=|5-（-3）|=8，EF=|4-（-7）|=11，所以由勾股定理可得：DE=
    		82+112
    =
    		185
    ．
    下面请你参与：
    （1）在图①中：AC=
    4
    4
    ，BC=
    3
    3
    ，AB=
    5
    5
    ．
    （2）在图②中：设A（x1，y1），B（x2，y2），试用x1，x2，y1，y2表示AC=
    y1-y2
    y1-y2
    ，BC=
    x1-x2
    x1-x2
    ，AB=
    		(x1-x2)2+(y1-y2)2
    		(x1-x2)2+(y1-y2)2
    ．
    （3）（2）中得出的结论被称为“平面直角坐标系中两点间距离公式”，请用此公式解决如下题目：
    已知：A（2，1），B（4，3），C为坐标轴上的点，且使得△ABC是以AB为底边的等腰三角形．请求出C点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图①，我们在“格点”直角坐标系上可以清楚看到：要找AB或DE的长度，显然是转化为求Rt△ABC或Rt△DEF的斜边长．

    下面：以求DE为例来说明如何解决：
    从坐标系中发现：D（-7，5），E（4，-3）．所以DF=|5-（-3）|=8，EF=|4-（-7）|=11，所以由勾股定理可得：DE=数学公式=数学公式．
    下面请你参与：
    （1）在图①中：AC=______，BC=______，AB=______．
    （2）在图②中：设A（x1，y1），B（x2，y2），试用x1，x2，y1，y2表示AC=______，BC=______，AB=______．
    （3）（2）中得出的结论被称为“平面直角坐标系中两点间距离公式”，请用此公式解决如下题目：
    已知：A（2，1），B（4，3），C为坐标轴上的点，且使得△ABC是以AB为底边的等腰三角形．请求出C点的坐标．

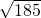    查看答案和解析>>

    科目：初中数学 来源： 题型：

    小知识：如图，我们称两臂长度相等（即）的圆规为等臂圆规. 当等臂圆规的两脚摆放在一条直线上时，若张角，则底角

    　

    请运用上述知识解决问题：

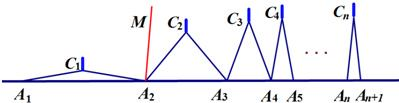
    　 如图，个相同规格的等臂圆规的两脚依次摆放在同一条直线上，其张角度数变化如下：

    ，， ，，…

    （1）①由题意可得=　　　　　 º；

    ②若 平分，则=　　　　　 º；

    （2）=　　　　　　　　　　　 º（用含的代数式表示）；

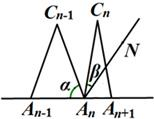
    （3）当时，设的度数为，的角平分线与构成的角的度数为，那么与之间的等量关系是　　　　　　　　　　　　 ，请说明理由. （提示：可以借助下面的局部示意图）

    查看答案和解析>>

    同步练习册答案