
分析 把等式$\frac{xy}{x+y}$=-2变形得到$\frac{x+y}{xy}$=-$\frac{1}{2}$,再把分母化为xyz得到$\frac{xz+yz}{xyz}$=-$\frac{1}{2}$,同样得到得$\frac{xy+xz}{xyz}$=$\frac{3}{4}$,$\frac{yz+xy}{xyz}$=-$\frac{3}{4}$,然后把三个分式相加可计算出所求分式的值.
解答 解:∵$\frac{xy}{x+y}$=-2,$\frac{yz}{y+z}$=$\frac{4}{3}$,$\frac{zx}{z+x}$=-$\frac{4}{3}$,
∴$\frac{x+y}{xy}$=-$\frac{1}{2}$,
∴$\frac{xz+yz}{xyz}$=-$\frac{1}{2}$,
同理可得$\frac{xy+xz}{xyz}$=$\frac{3}{4}$,$\frac{yz+xy}{xyz}$=-$\frac{3}{4}$,
∴$\frac{xz+yz}{xyz}$+$\frac{xy+xz}{xyz}$+$\frac{yz+xy}{xyz}$=-$\frac{1}{2}$+$\frac{3}{4}$-$\frac{3}{4}$=-$\frac{1}{2}$,
∴$\frac{xy+yz+xz}{xyz}$=-$\frac{1}{4}$.
故答案为-$\frac{1}{4}$.
点评 本题考查了分式的化简求值:根据所求代数式的结构特点,通过变形已知条件化为同分母的分式,然后进行分式的加法运算.


科目:初中数学 来源: 题型:解答题
 如图所示,有一个长为4cm、宽为3cm的长方形.
如图所示,有一个长为4cm、宽为3cm的长方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
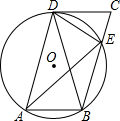 如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.
如图,在?ABCD中,过A、B、D三点的⊙O交BC于点E,连接DE,∠CDE=∠DAE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BC表示河岸,现测得∠ACB=30°,∠ABC=45°,AC=20米,某人位于河岸上的P处,
如图,BC表示河岸,现测得∠ACB=30°,∠ABC=45°,AC=20米,某人位于河岸上的P处,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com