
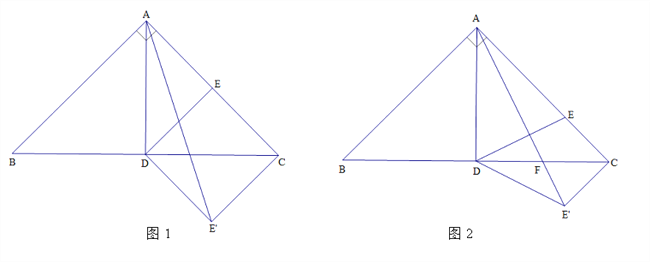
【题目】在等腰直角三角形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是斜边
是斜边![]() 的中点,连接
的中点,连接![]() .
.
(1)如图1, ![]() 是
是![]() 的中点,连接
的中点,连接![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() ,连接
,连接![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)如图2,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() 的值为
的值为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)在等腰直角三角形中先求出AC的长,再在Rt△ACE′中,理由勾股定理求出AE′的长即可;(2)B作AE’的垂线交AD于点G,交AC于点H,由角角边可证△ABH≌△CAE′,所以AH=HE=CE,进而D是BC中点,由中位线定理得DE//BH ,再由角角边得△ABG≌△CAF,得到AG=CF进而DF=CF.
试题解析:(1)∵![]() ,
, ![]() ,D是斜边
,D是斜边![]() 的中点,
的中点,
∴![]() ,∠ACD=45°,
,∠ACD=45°,
在RtADC中:AC=AD.sin45°=![]()
∵E是AC的中点
∴CE=![]() AC=
AC=![]()
∵将△CDE沿CD翻折到△CDE′
∴CE′=CE=![]() , ∠ACE′=90°,由勾股定理得:
, ∠ACE′=90°,由勾股定理得:
AE′=![]()
过B作AE’的垂线交AD于点G,交AC于点H

∵∠ABH+∠BAF=90°,∠CAF+∠BAF=90°
∴∠ABH=∠CAF
又∵AB=AC,∠BAH=∠ACE’=90°
∴△ABH≌△CAE′
∴AH=CE′=CE
∵![]()
∴AH=HE=CE
∵D是BC中点
∴DE//BH
∴G是AD中点
在ABG和CAF中:AB=AC,∠BAD=∠ACD=45°,∠ABH=∠CAF
∴△ABG≌△CAF
∴AG=CF
∵AG=![]() AD
AD
∴CF=![]() AD=
AD=![]() CD
CD
∴DF=CF


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
. 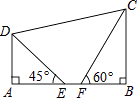
(1)BC= .
(2)求点D到BC的距离.
(3)求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“书香校园”号召,重庆一中在九年级学生中随机抽取某班学生对2016年全年阅读中外名著的情况进行调查,整理调查结果发现,每名学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的折线统计图和扇形统计图.
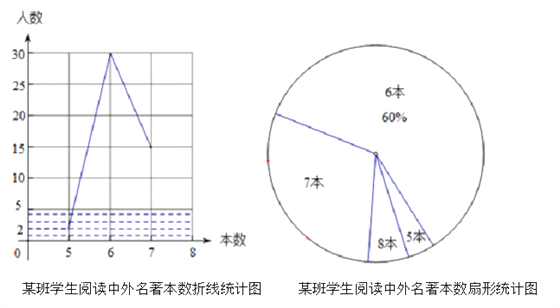
(1)该班学生共有 名,扇形统计图中阅读中外名著本数为7本所对应的扇形圆心角的度数是 度,并补全折线统计图;
(2)根据调查情况,班主任决定在阅读中外名著本数为5本和8本的学生中任选两名学生进行交流,请用树状图或表格求出这两名学生阅读的本数均为8本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数![]() 都可以进行这样的分解:
都可以进行这样的分解: ![]() (
(![]() ,
, ![]() 是正整数,且
是正整数,且![]() ),在
),在![]() 的所有这种分解中,如果
的所有这种分解中,如果![]() ,
, ![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是
是![]() 的最佳分解,并规定:
的最佳分解,并规定: ![]() .
.
例如![]() 可以分解成
可以分解成![]() ,
, ![]() 或
或![]() ,因为
,因为![]() ,所以
,所以![]() 是
是![]() 的最佳分解,所以
的最佳分解,所以![]() .
.
(![]() )求出
)求出![]() 的值.
的值.
(![]() )如果一个两位正整数
)如果一个两位正整数![]() ,
, ![]() (
(![]() ,
, ![]() ,
, ![]() 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为
为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为![]() ,那么我们称这个数
,那么我们称这个数![]() 为“文澜数”,求所有“文澜数”并写出所有“文澜数”中
为“文澜数”,求所有“文澜数”并写出所有“文澜数”中![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用描点法画二次函数y=ax2+bx+c(a≠0)的图象时,列出了如下表格:
x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
y=ax2+bx+c(a≠0) | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
那么当该二次函数值y > 0时,x的取值范围是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[实际情境]李明家、王亮家、西山森林公园都位于石家庄市槐安路的沿线上,李明、王亮同学时分别从自己家出发,沿笔直的槐安路匀速骑行到达西山森林公园,李明的骑行速度是王亮的骑行速度的1.5倍.
[数学研究]设t(分钟)后李明、王亮两人与王亮家的距离分别为y1 . y2 , 则y1 . y2与t的函数关系图象如图所示,试根据图象解决下列问题: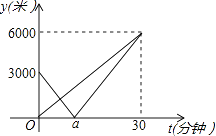
(1)填空:王亮的速度v2=米/分钟;
(2)写出y1与t的函数关系式;
(3)因为李明携带的无线对讲机电量不足,只有在小于1000米范围内才能和王亮的无线对讲机清晰地通话,试探求什么时间段内两人的无线对讲机无法清晰通话.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com