
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;(2)若CD=1,求AD的长.

【答案】(1)证明见解析 (2)![]()
【解析】
(1)先利用等腰直角三角形的性质及角的等量替换证明△ADC≌△BDF,得到BF=AC再根据等腰三角形三线合一得出AC=2AE,即可得证;
(2)在在Rt△CDF,利用勾股定理求出CF,再利用等腰三角形的性质得AF=CF,即可求出AD.
(1)证明:∵AD⊥BC,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,AD⊥BC,
∴∠CAD+∠ACD=90°,∠CBE+∠ACD=90°,
∴∠CAD=∠CBE,
在△ADC和△BDF中,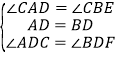 ,
,
∴△ADC≌△BDF(ASA),
∴BF=AC,
∵AB=BC,BE⊥AC,
∴AC=2AE,
∴BF=2AE;
(2)解:∵△ADC≌△BDF,
∴DF=CD=1,
在Rt△CDF中,CF=![]()
∵BE⊥AC,AE=EC,
∴AF=CF=![]() ,
,
∴AD=AF+DF=1+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD∽四边形GFEH,且∠A=∠G=70°,∠B=55°,∠E=120°,DC=20,HE=15,HG=21.求∠D,∠F的大小和AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD为∠BAC的平分线,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC交AC的延长线于F.

(1)求证:BE=CF;
(2)如果AB=7,AC=5,求AE,BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,点E在BA的延长线上,点D在BC边上,且ED=EC,若△ABC的边长为4,AE=2,则BD的长为( )

A. 2 B. 3 C. ![]() D.
D. ![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,线段m,用尺规作图作菱形ABCD,使它的边长为m,一个内角等于
,线段m,用尺规作图作菱形ABCD,使它的边长为m,一个内角等于![]() 其具体步骤如下:
其具体步骤如下:

![]()

![]() 作
作![]() ;
;
![]() 以点A为圆心,线段m长为半径画弧,交AE于点B,交AF于点D;
以点A为圆心,线段m长为半径画弧,交AE于点B,交AF于点D;
![]() __________;
__________;
![]() 连接BC、DC,则四边形ABCD为所作的菱形
连接BC、DC,则四边形ABCD为所作的菱形![]() 第
第![]() 步应为
步应为![]()
![]()
A. 分别以点B、D为圆心,以AF长为半径画弧,两弧交于点C
B. 分别以点E、F为圆心,以AD长为半径画弧,两弧交于点C
C. 分别以点B、D为圆心,以AD长为半径画弧,两弧交于点C
D. 分别以点E、F为圆心,以AF长为半径画弧,两弧交于点C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CBD、∠BCE是△ABC的外角,BP平分∠ABC,CP平分∠ACB,BQ平分∠CBD,CQ平分∠BCE.
(1)∠PBQ的度数是 ,∠PCQ的度数是 ;
(2)若∠A=70°,求∠P和∠Q的度数;
(3)若∠A=α,则∠P= ,∠Q= (用含α的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题)
如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB.∠EDF=90°,点D在直线l上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系.

(探究发现)
(1)如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点D移动到使点P与点C重合时,通过推理就可以得到DP=DB,请写出证明过程;
(数学思考)
(2)如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,这个小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程;
(拓展引申)
(3)如图4,在(1)的条件下,M是AB边上任意一点(不含端点A、B),N是射线BD上一点,且AM=BN,连接MN与BC交于点Q,这个数学兴趣小组经过多次取M点反复进行实验,发现点M在某一位置时BQ的值最大.若AC=BC=4,请你直接写出BQ的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为
为![]() 上的一点,按下列要求进行作图.
上的一点,按下列要求进行作图.
(1)作![]() 的平分线
的平分线![]() .
.
(2)在![]() 上取一点
上取一点![]() ,使得
,使得![]() .
.
(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边![]() 上取一点
上取一点![]() ,使得
,使得![]() ,这时他发现
,这时他发现![]() 与
与![]() 之间存在一定的数量关系,请写出
之间存在一定的数量关系,请写出![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设 A 是由n×n 个有理数组成的n 行n 列的数表, 其中aij ( i,j =1,2,3,,n )表示位于第i 行第 j 列的数,且aij 取值为 1 或-1.
a | a | a | |
a | a | a | |
a | a | a |
对于数表 A 给出如下定义:记 xi 为数表 A 的第i 行各数之积,y j 为数表 A 的第 j 列各数之积.令S = (x1+ x2++ x![]() )+(y1+ y2+ y
)+(y1+ y2+ y![]() ),将S 称为数表 A 的“积和”.
),将S 称为数表 A 的“积和”.
(1)当n = 4 时,对如下数表 A,求该数表的“积和” S 的值;
1 | 1 | -1 | -1 |
1 | -1 | 1 | 1 |
1 | -1 | -1 | 1 |
-1 | -1 | 1 | 1 |
(2)是否存在一个 3×3 的数表 A,使得该数表的“积和” S =0 ?并说明理由;
(3)当n =10 时,直接写出数表 A 的“积和” S 的所有可能的取值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com