
����Ŀ���ܡ��¹ڡ������Ӱ�죬ij����������������![]() ��
��![]() �����ͺŵġ���д�塱�������ķᣮ��֪
�����ͺŵġ���д�塱�������ķᣮ��֪![]() �ͣ�
�ͣ�![]() ����д����ۡ��ۼۺ�ÿ�������������ʾ��
����д����ۡ��ۼۺ�ÿ�������������ʾ��
���ۣ�Ԫ/���� | �ۼۣ�Ԫ/���� | ��������/�գ� | |
|
|
|
|
|
|
|
|
�����г����飬�������̶�![]() ����д�彵�����ۣ�ͬʱ��
����д�彵�����ۣ�ͬʱ��![]() ����д������ۼۣ���ʱ����
����д������ۼۣ���ʱ����![]() ����д��ÿ����
����д��ÿ����![]() Ԫ�Ϳɶ���
Ԫ�Ϳɶ���![]() ����
����![]() ����д��ÿ���
����д��ÿ���![]() Ԫ������
Ԫ������![]() ����Ҫ����ÿ�������������䣬������
����Ҫ����ÿ�������������䣬������![]() ����д��ÿ�������
����д��ÿ�������![]() ����ÿ���ܻ���������Ϊ
����ÿ���ܻ���������Ϊ![]() Ԫ
Ԫ
��1����![]() ��
��![]() ֮��ĺ�����ϵʽ��д��
֮��ĺ�����ϵʽ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��Ҫʹÿ���������![]() Ԫ��ֱ��д��
Ԫ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3���������̾���ÿ����һ��![]() ����д�壬�;�
����д�壬�;�![]() Ԫ��
Ԫ��![]() ���¹����顱Ӱ������Ѽ�ͥ����
���¹����顱Ӱ������Ѽ�ͥ����![]() ʱ��ÿ����������Ϊ
ʱ��ÿ����������Ϊ![]() Ԫ����
Ԫ����![]() ��ֵ��
��ֵ��
���𰸡���1��![]() ��
��![]() ������x��������2��
������x��������2��![]() ����x��������3��
����x��������3��![]()
��������
��1����![]() ����д��ÿ�������
����д��ÿ�������![]() ������B����д��ÿ��������
������B����д��ÿ��������![]() ���������ܻ���������
���������ܻ���������![]() ��������A����д�����������������B����д������������ÿ�����۵�����ÿ�յ�������Ϊ�Ǹ�����
��������A����д�����������������B����д������������ÿ�����۵�����ÿ�յ�������Ϊ�Ǹ�����![]() Ϊ�Ǹ��������x��ȡֵ��Χ��
Ϊ�Ǹ��������x��ȡֵ��Χ��
��2����ϣ�1�����������������䷽�������![]() ʱ��xֵ�����ͼ��õ�ÿ���������
ʱ��xֵ�����ͼ��õ�ÿ���������![]() Ԫʱ��x��ȡֵ��Χ��������⣻
Ԫʱ��x��ȡֵ��Χ��������⣻
��3�������ÿ�������Ϊ![]() Ԫ����
Ԫ����![]() ��Ȼ�����ö��κ��������ʽ�����⣮
��Ȼ�����ö��κ��������ʽ�����⣮
�⣺��1�� ![]() ��
��
����ã�![]() ��
��
������֪��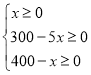 ��
��
��ã�![]() ��
��
��![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ��
��![]() ������
������
��2��![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ��
��
�������£�![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
Ҫʹ![]() ����ͼ��֪��
����ͼ��֪��![]() ��
��
![]() ��
��
![]() ����
����![]() ������
������
��3�������ÿ�������Ϊ![]() Ԫ��
Ԫ��
��![]() ��
��
�Գ���Ϊ![]() ��
��
![]() ��
��
![]() ��
��
![]() �����߿������£���
�����߿������£���![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
��![]() ʱ��
ʱ��![]() ���
���
![]() ��
��
��ã�![]() ��
��


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���DΪ��BC��һ�㣬��AD��AB��AE��BC������Ϊ��E������D��DF��AB������AC�ڵ�F������EF��EF2��![]() BDEC��
BDEC��
(1)��֤����EDF�ס�EFC��
(2)���![]() ����֤��AB��BD��
����֤��AB��BD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
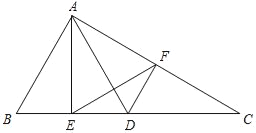
����Ŀ��ij��ѧ��ί��Ϊ�о���Уѧ���Ŀ����������ȡ�����ķ��������Ķ����˶������֡��������ĸ����������������ѧ������Ȥ���ã���������Ľ�����������µ�������������ͳ��ͼ����ͼ1��ͼ2�����������ͼ���ṩ����Ϣ����������⣺
��1��������о��У�һ�������˶�����ѧ����
��2����������������ͼ����ռ��Բ�Ľ��Ƕ��ٶȣ�
��3����ȫƵ���ֲ�����ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
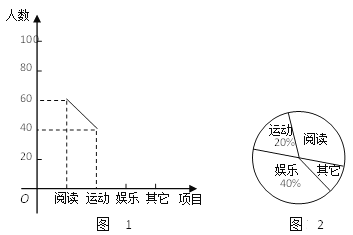
����Ŀ���ı��ε�һ���Խ��߽�����ı��ηֳ����������Σ��������������������(��ȫ��)����ô���ǽ������Խ��߽�������ı��ε����ƶԽ��ߣ�
(1)��ͼ1���ı���ABCD�У���DAB��100������DCB��130�����Խ���ACƽ�֡�DAB����֤��AC���ı���ABCD�����ƶԽ��ߣ�
(2)��ͼ2��ֱ��![]() �ֱ���x��y���ཻ��A��B���㣬PΪ����������y��
�ֱ���x��y���ཻ��A��B���㣬PΪ����������y��![]() (k��0)�ϵĵ㣬��AO���ı���ABOP�����ƶԽ��ߣ����������Ľ���ʽ��
(k��0)�ϵĵ㣬��AO���ı���ABOP�����ƶԽ��ߣ����������Ľ���ʽ��
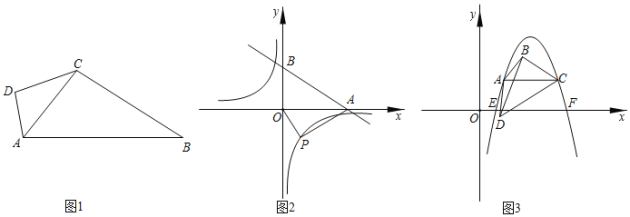
(3)��ͼ3��AC���ı���ABCD�����ƶԽ��ߣ���C������Ϊ(3��1)��AC��x�ᣬ��BCA����DCA��30��������BD����BCD�����Ϊ![]() ����A��C�����������y��ax2+bx+c(a��0)��x�ύ��E��F���㣬��|m|��AC+1����ֱ��y��mx��������ǡ����3�����㣬��ʵ��a��ֵ��
����A��C�����������y��ax2+bx+c(a��0)��x�ύ��E��F���㣬��|m|��AC+1����ֱ��y��mx��������ǡ����3�����㣬��ʵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
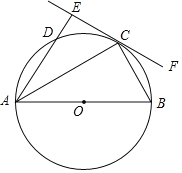
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() �����
�����![]() �غϣ�������
�غϣ�������![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ������Ϊ
������Ϊ![]() ��
��
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() ��
��
����![]() �İ뾶��
�İ뾶��
������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() _____��
_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y����kx+m��˫����y��![]() ��x��0������A��B���㣬��A�ĺ�����Ϊ1����B��������Ϊ2����P��y����һ���㣬����PAB���ܳ���Сʱ����P��������_______��
��x��0������A��B���㣬��A�ĺ�����Ϊ1����B��������Ϊ2����P��y����һ���㣬����PAB���ܳ���Сʱ����P��������_______��
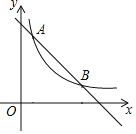
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
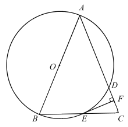
����Ŀ����ͼ��ABΪ��O��ֱ����C��DΪ��O�ϵ����㣬��BAC����DAC������C��ֱ��EF��AD����AD���ӳ����ڵ�E������BC��
��1����֤��EF�ǡ�O�����ߣ�
��2������CAO��30����BC��2�����ӻ�BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�![]() ��
��![]() ��
��![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ�����㣬����
�ϵ�һ�����㣬����![]() ������
������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() �˶���
�˶���![]() ʱ����
ʱ����![]() ��֮�˶������
��֮�˶������![]() ������Ϊ
������Ϊ![]() ����
����![]() ��ȡֵ��Χ��_____��
��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����Ӳ�Ʒר����20Ԫ/���ļ۸�������ij�¿��������������60������������������������
��������(��x��) | �ۼ�(Ԫ) | ��������(��) |
1��x��35 | x+30 | 100��2x |
35��x��60 | 70 | 100��2x |
(1)��������ÿ�������ΪWԪ�����W��x�ĺ�����ϵʽ��
(2)�����������ε���һ����������W���Դﵽ���ֵ�����ֵΪ���٣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com