
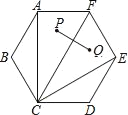
【题目】如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
A. 1 B. 2 C. 2![]() ﹣2 D. 4﹣2
﹣2 D. 4﹣2![]()
【答案】C
【解析】
先判断出PQ⊥CF,再求出AC=2![]() ,AF=2,CF=2AF=4,利用△ACF的面积的两种算法即可求出PG,然后计算出PQ即可.
,AF=2,CF=2AF=4,利用△ACF的面积的两种算法即可求出PG,然后计算出PQ即可.
解:如图,连接PF,QF,PC,QC

∵P、Q两点分别为△ACF、△CEF的内心,
∴PF是∠AFC的角平分线,FQ是∠CFE的角平分线,
∴∠PFC=![]() ∠AFC=30°,∠QFC=
∠AFC=30°,∠QFC=![]() ∠CFE=30°,
∠CFE=30°,
∴∠PFC=∠QFC=30°,
同理,∠PCF=∠QCF
∴PQ⊥CF,
∴△PQF是等边三角形,
∴PQ=2PG;
易得△ACF≌△ECF,且内角是30,60,90的三角形,
∴AC=2![]() ,AF=2,CF=2AF=4,
,AF=2,CF=2AF=4,
∴S△ACF=![]() AF×AC=
AF×AC=![]() ×2×2
×2×2![]() =2
=2![]() ,
,
过点P作PM⊥AF,PN⊥AC,PQ交CF于G,
∵点P是△ACF的内心,
∴PM=PN=PG,
∴S△ACF=S△PAF+S△PAC+S△PCF
=![]() AF×PM+
AF×PM+![]() AC×PN+
AC×PN+![]() CF×PG
CF×PG
=![]() ×2×PG+
×2×PG+![]() ×2
×2![]() ×PG+
×PG+![]() ×4×PG
×4×PG
=(1+![]() +2)PG
+2)PG
=(3+![]() )PG
)PG
=2![]() ,
,
∴PG=![]() =
=![]() ,
,
∴PQ=2PG=2(![]() )=2
)=2![]() -2.
-2.
故选C.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】机器人“海宝”在某圆形区域表演“按指令行走”,如图所示,“海宝”从圆心O出发,先沿北偏西67.4°方向行走13米至点A处,再沿正南方向行走14米至点B处,最后沿正东方向行走至点C处,点B、C都在圆O上.
(1)求弦BC的长;
(2)求圆O的半径长.
(本题参考数据:sin 67.4° =![]() ,cos 67.4°=
,cos 67.4°=![]() ,tan 67.4° =
,tan 67.4° =![]() )
)
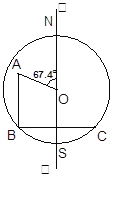
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1:y1=x+b经过点A(﹣5,0),交y轴于点B,直线l2:y2=﹣2x﹣4与直线l1:y1=x+b交于点C,交y轴于点D.

(1)求b的值;
(2)求△BCD的面积;
(3)当0≤y2<y1时,则x的取值范围是 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC, BD相交于点O, OB=OD.要使△AOB≌△COD,则下列添加的条件中错误的是( )

A.∠A=∠CB.∠B=∠DC.OA=OCD.AB=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
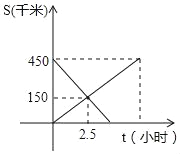
【题目】甲、乙两地之间的铁路交通设有特快列车和普通快车两种车次,某天一辆普通快车从甲地出发匀速向乙地行驶,同时另一辆特快列车从乙地出发匀速向甲地行驶,两车离甲地的路程S(千米)与行驶时间t(时)之间的函数关系如图所示.
(1)甲地到乙地的路成为________千米,普通快车到达乙地所用时间为_______小时.
(2)求特快列车离甲地的路程s与t之间的函数关系式.
(3)在甲、乙两地之间有一座铁路桥,特快列车到铁路桥后又行驶0.5小时与普通快车相遇,求甲地与铁路桥之间的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、点
、点![]() ,
,![]() ,若将
,若将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,折痕
重合,折痕![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)求点![]() 的坐标;
的坐标;
(3)求直线![]() 的表达式.
的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,李老师让同学们试着用角尺平分 ![]() (如图所示),有两组.
(如图所示),有两组.

同学设计了如下方案:
方案①:将角尺的直角顶点![]() 介于射线
介于射线![]() 之间,移动角尺使角尺两边相同的刻度位于
之间,移动角尺使角尺两边相同的刻度位于![]() 上,且交点分别为
上,且交点分别为![]() ,即
,即![]() ,过角尺顶点
,过角尺顶点![]() 的射线
的射线![]() 就是
就是![]() 的平分线.
的平分线.
方案②:在边![]() 上分别截取
上分别截取![]() ,将角尺的直角顶点
,将角尺的直角顶点![]() 介于射线
介于射线![]() 之间,移动角尺使角尺两边相同的刻度与点
之间,移动角尺使角尺两边相同的刻度与点![]() 重合,即
重合,即![]() ,过角尺顶点
,过角尺顶点![]() 的射线
的射线![]() 就是
就是![]() 的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从宁海县到某市,可乘坐普通列车或高铁,已知高铁的行驶路程与普通列车的行驶路程之和是920千米,而普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车的平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com