
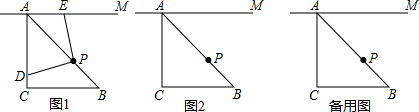
分析 (1)先判断出∠HPF=90°,进而判断出∠HPD=∠FPE,再判断出PH=PF,得到△PHD≌△PFE即可;
(2)依题意画出图形,由(1)得到△PHD≌△PFE.再判断出△BAC≌△BDC,求出AP=$3\sqrt{2}$.AH=3,进而求出AE;
(3)先表示出HD=x-3.EF=x-3.AE=6-x.再判断出∠EPG=∠DPG.得出△GDP≌△GEP.在Rt△AGE中,GE2=AG2+AE2,即y2=(x-y)2+(6-x)2,即可.
解答 解:(1)证明:如图1,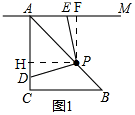
作PH⊥AC于H,作PF⊥AM于F,
∵AC⊥BC,AM∥CB,
∴AC⊥AM.
∵∠AHP+∠HAF+∠AFP+∠FPH=360°,
∴∠HPF=90°.
∵PE⊥PD,即∠DPE=90°,
∴∠HPD=∠FPE.
∵AC⊥BC,AC=BC,
∴∠CAB=∠CBA=45°.
∵AM∥CB,
∴∠MAB=∠CBA=45°.
∴∠CAB=∠BAM.
∴PH=PF.
∴△PHD≌△PFE.
∴PD=PE.
(2)解:如图2,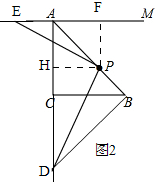
作PH⊥AC于H,作PF⊥AM于F,同(1)得△PHD≌△PFE.
∴DH=EF.
∵BA=BD,∠ACB=∠DCB=90°,BC=BC,
∴△BAC≌△BDC.
∴CD=CA=4.
∵AC⊥BC,AC=BC=4,
∴AB=$4\sqrt{2}$.
∵BP=$\sqrt{2}$,
∴AP=$3\sqrt{2}$.
∵PH⊥AC,∠CBA=45°,
∴HP=AH=3,
∴DH=AD-AH=8-3=5.
∴EF=5.
∵在四边形AHPF中,PH⊥AC,PF⊥AC,AC⊥BC,
∴AHPF是矩形.
∴AF=HP=3.
∴AE=EF-AF=5-3=2.
(3)如图3,
作PH⊥AC于H,作PF⊥AM于F,由(2)得DH=EF.
∵∠CAB=45°,∴HA=HP=3,
∴HD=x-3.
∴EF=x-3.
∴AE=6-x.
∵PG平分∠EPD,
∴∠EPG=∠DPG.
∵PD=PE,GP=GP,
∴△GDP≌△GEP.
∴GE=GD=y.
在Rt△AGE中,GE2=AG2+AE2,即y2=(x-y)2+(6-x)2,
∴$y=x+\frac{18}{x}-6$(x≥3).
点评 此题是三角形综合题,主要考查了全等三角形的性质和判定,矩形的判定和性质,同角的余角相等,勾股定理,解本题的关键是判断△PHD≌△PFE.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
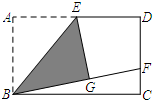 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )| A. | 6$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{5}$ | D. | 4$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{625}$ | C. | -$\frac{1}{5}$或$\frac{1}{5}$ | D. | $\frac{1}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com