
分析 (1)根据题意可以利用分类讨论的数学思想解答本题;
(2)根据(1)中的答案和题意可以分别求得各种方案下的利润,然后进行比较即可解答本题.
解答 解:(1)设甲、乙、丙三种型号的电视机分别购买x台、y台、z台,
若购进甲、乙两种型号的电视机,
$\left\{\begin{array}{l}x+y=50\\ 1200x+2000y=80000\end{array}\right.$,
解得,$\left\{\begin{array}{l}x=25\\ y=25\end{array}\right.$,
若购进甲、丙两种型号的电视机,
$\left\{\begin{array}{l}x+z=50\\ 1200x+2200z=80000\end{array}\right.$,
解得,$\left\{\begin{array}{l}x=30\\ z=20\end{array}\right.$,
若购进乙、丙两种型号的电视机,
$\left\{\begin{array}{l}y+z=50\\ 2000y+2200z=80000\end{array}\right.$,
解得,$\left\{\begin{array}{l}y=150\\ z=-100\end{array}\right.$(舍去),
故该商场有两种进货方案,即
方案一:购买25台甲型电视和25台乙型电视,
方案二:购买30台甲型电视和20台丙型电视;
(2)若按方案一进货,利润为:200×25+250×25=11250(元),
若按方案二进货,利润为:200×30+300×20=12000(元),
∵12000>11250,
∴按方案二:购买30台甲型电视和20台丙型电视进货,可获利最大,最大利润为12000元,
答:按方案二:购买30台甲型电视和20台丙型电视进货,可获利最大,最大利润为12000元.
点评 本题考查二元一次方程组的应用,解答本题的关键是明确题意,列出相应的方程组,利用分类讨论的数学思想解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
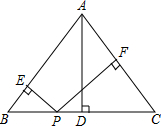 在△ABC中,AB=AC=10,BC=12,BC边上高AD=8,P为BC边上一动点,PE⊥AB于E,PF⊥AC于F.
在△ABC中,AB=AC=10,BC=12,BC边上高AD=8,P为BC边上一动点,PE⊥AB于E,PF⊥AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com